Lecture 12:

DATA 101: Making Prediction with Data

Dr. Irene Vrbik

University of British Columbia Okanagan

Introduction

• In the last lecture we saw how we could fit the KNN classification models using tidymodels.
• Recall: tidymodels is an R package and framework for modeling that follows the principles of the tidyverse.
• In the upcoming lectures we will continue to work with tidymodels to tackle the regression problem
• In other words, we focus on predicting numeric variables in contrast to previous lectures which concentrated on predicting a categorical variable (classification problem).

Similarities with Classification:

• Regression, like classification, is a predictive problem setting where we want to use past information to predict future observations.
• Just like in the classification setting, there are many possible methods that we can use to predict numerical response variables.
• In this chapter we will focus on the K-nearest neighbors (KNN) algorithm

• next up: linear regression

In your future studies, you might encounter regression trees, splines, and general local regression methods; see the additional resources section at the end ch 8 to begin learning more about these (optional) other methods.

Regression vs. Classification

Goal of Classification: predict a categorical or discrete label or class.

Example applications: spam detection, image recognition , sentiment analysis, and medical diagnosis. The output is often a class label, and the model’s objective is to assign input data points to the correct class.

Goal of Regression: predict a continuous or numeric value.

Example applications: predicting house prices based, forecasting stock prices, estimating a person’s age from facial features, and predicting a person’s income based on various factors.

• The output variable is divided into predefined classes or categories.
• (classifying emails as spam or not)
• image dog/cat (identifying objects in images)
• sentiment: (categorizing text as positive, negative, or neutral)
• diagnosis: (classifying diseases based on patient symptoms)

Regression

• house: based on features like square footage, number of bedrooms, etc., forecasting stock prices, estimating a person’s age from facial features, and predicting a person’s income based on various factors.
• The output is typically a real number, and the model’s objective is to estimate this numeric value accurately.

Similarity of methods

While this lecture will tackle a different mode of problems, the following will be the same:

• Data splitting into training, validation, and test sets.
• Utilization of tidymodels workflows for a structured approach.
• Adoption of K-nearest neighbors (KNN) for making predictions.
• Implementation of cross-validation for hyperparameter tuning.

KNN for regression

• Many of the concepts from classification map over to the setting of regression.
• For example, a regression model predicts a new observation’s response variable based on the response variables for similar observations in the training set (as indicated in the nearest neighbourhood)
• As before the best choice for the number of nearest neighbours to choose from will be determined by cross-validation (CV)

Data

• We will study a data set of real estate transactions originally reported in the Sacramento Bee newspaper. [Source]

• It comprises 932 transactions in Sacramento, California over a five-day period

library(tidyverse)
library(tidymodels)
library(gridExtra)
set.seed(5)
(sacramento <- read_csv("data/sacramento.csv"))

Data

Motivating Question

• Our question is again predictive: Can we use the size of a house in the Sacramento, CA area to predict its sale price?
• A rigorous, quantitative answer to this question might help a realtor advise a client as to whether the price of a particular listing is fair, or perhaps how to set the price of a new listing.

We first need to formulate a precise question that we want to answer.

Exploratory Data Analysis

• For our initial exploration, let’s investigate the relationship between sqft (house size, in livable square feet) and price (house sale price, in US dollars (USD)).
• Let’s create a scatter plot with the predictor variable (house size) on the x-axis, and we place the response variable that we want to predict (sale price) on the y-axis.

eda <- ggplot(sacramento, aes(x = sqft, y = price)) +
  geom_point(alpha = 0.4) +
  xlab("House size (square feet)") +
  ylab("Price (USD)") +
  scale_y_continuous(labels = dollar_format()) + # add $ and ,s
  theme(text = element_text(size = 12))

format the y-axis labels to put dollar signs and commas

Scatterplot

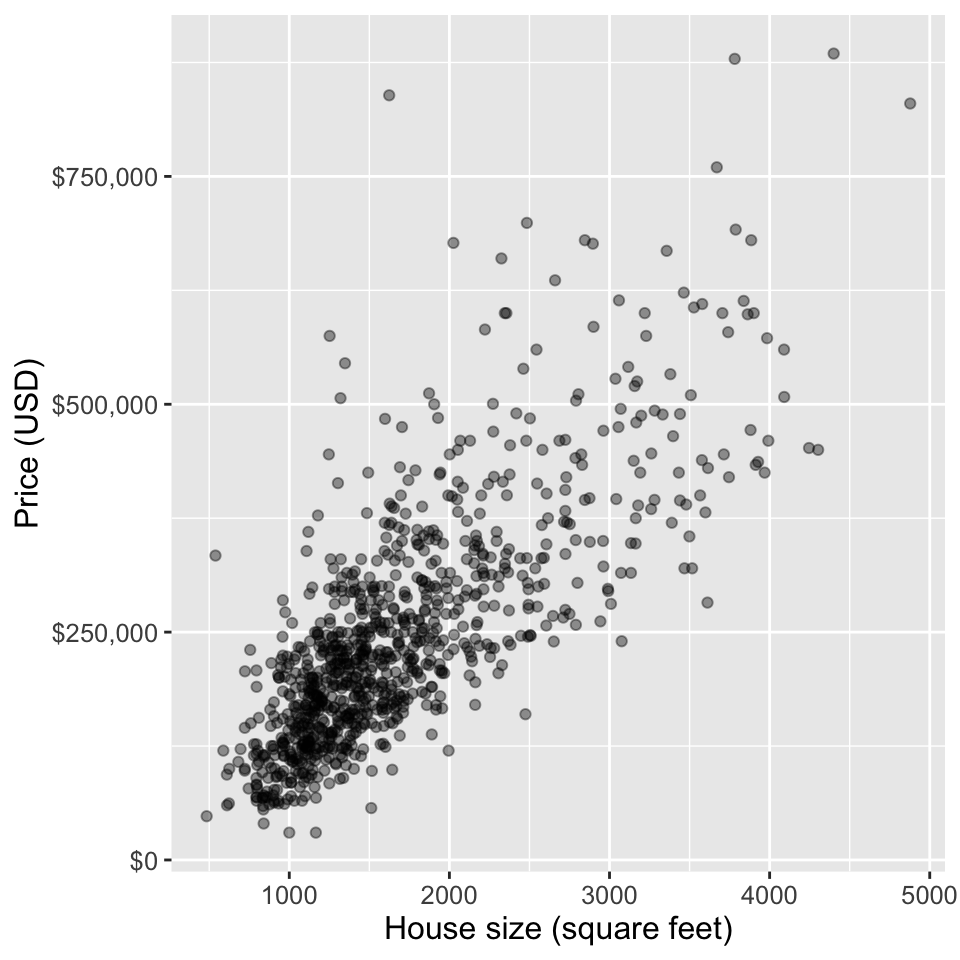
• We can see that in Sacramento, CA, as the size of a house increases, so does its sale price.
• Thus, we can reason that we may be able to use the size of an unsold to predict its final sale price.

K-Nearest Neighbour Regression

Much like in the case of classification, we can use a K-nearest neighbors-based approach in regression to make predictions.

1. Select the number K of the neighbors.
2. Find the K nearest¹ neighbors
3. Compute the average price among these K neighbors

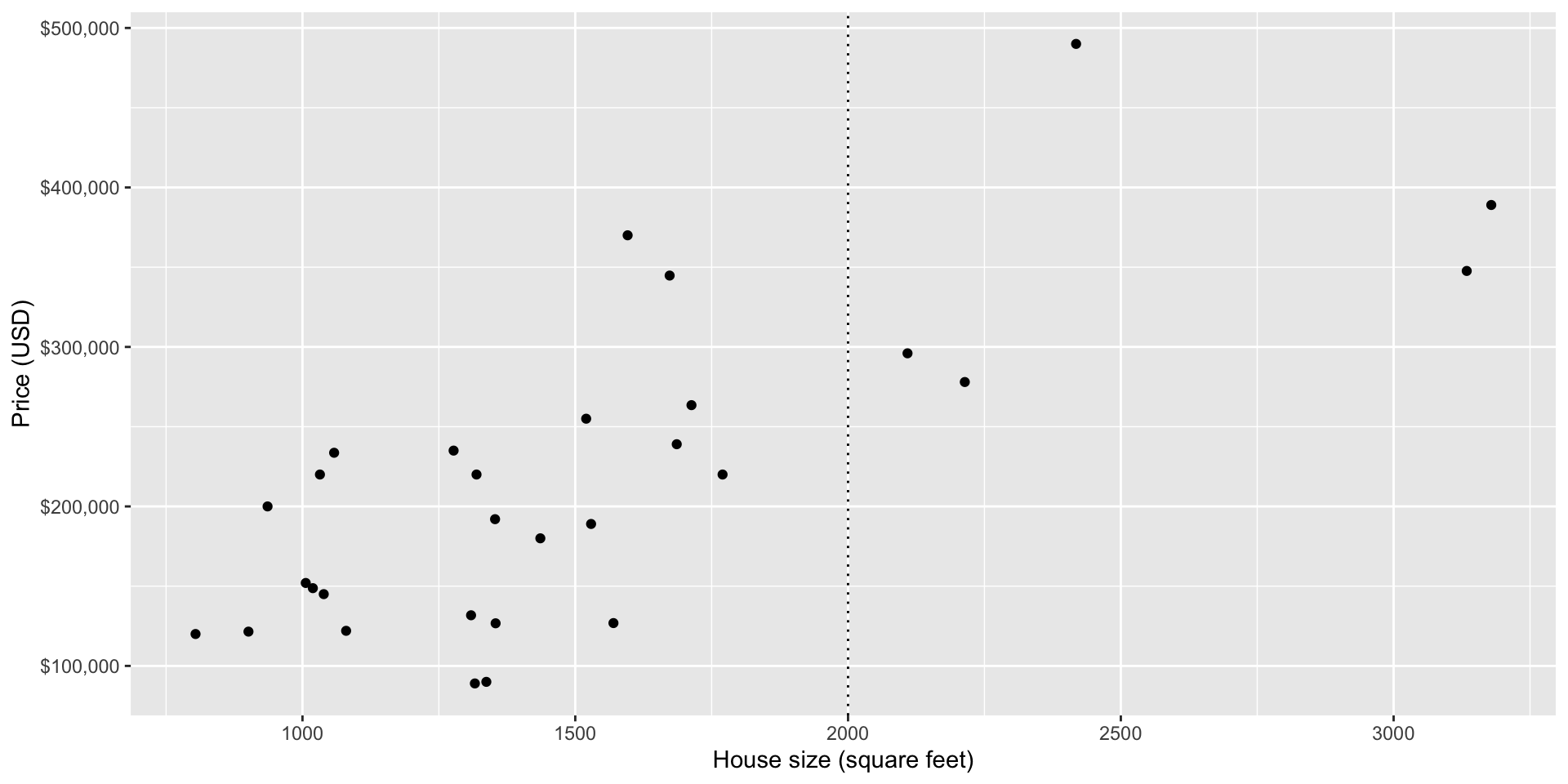
Let’s take a small sample of the data to illustrate the mechanics of KNN regression …

1. as per the calculated Euclidean distance; recall it is advisable to scale your data

Random Sample

• To take a small random sample of size 30, we’ll use the function slice_sample, and input the data frame to sample from and the number of rows to randomly select.

set.seed(2023101)
small_sacramento <- slice_sample(sacramento, n = 30)

• Based on the sample data above, what would we predict the selling price of a 2000 square foot house?

Note this is slightly different than the textbook since I don’t know what seed they used!

Small plot

small_plot <- ggplot(small_sacramento, aes(x = sqft, y = price)) +
  geom_point() +
  xlab("House size (square feet)") +
  ylab("Price (USD)") +
  scale_y_continuous(labels = dollar_format()) +
  geom_vline(xintercept = 2000, linetype = "dotted") 

The geom_*line geoms add reference lines (sometimes called rules) to a plot, either horizontal (geom_hline), vertical (geom_vline), or diagonal (geom_abline) (specified by slope and intercept).

These are useful for annotating plots.

Nearest Neighbours

Suppose we were employing KNN regression with K = 5 (we’ll come back to this later)

(nearest_neighbors <- small_sacramento |>
  mutate(diff = abs(2000 - sqft)) |>
  slice_min(diff, n = 5))

Nearest Neighbours

Code

small_plot + geom_segment(data = nearest_neighbors, 
                          aes(x = sqft, xend = 2000, 
                              y = price, yend = price), 
                          color = "orange")

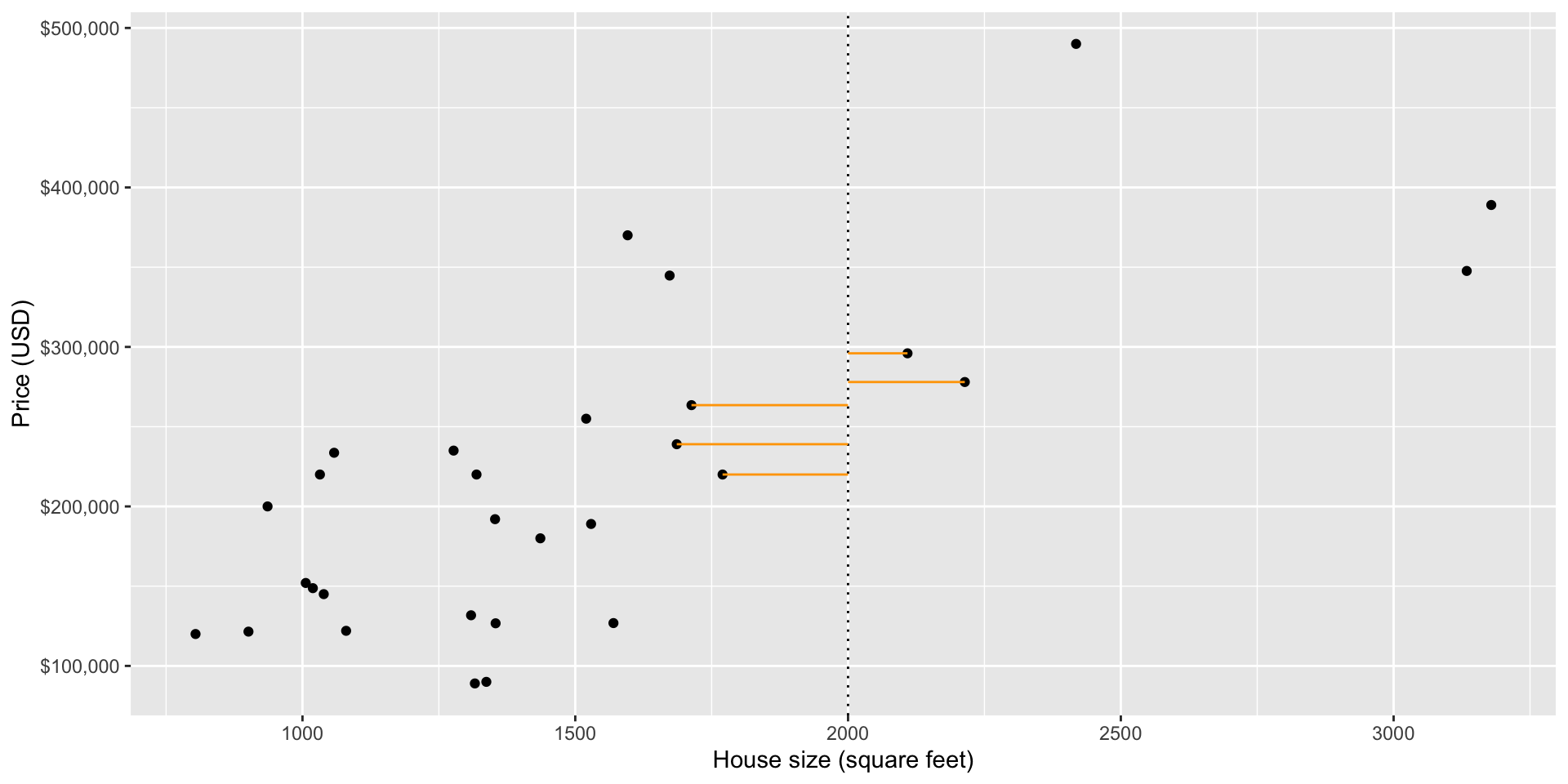
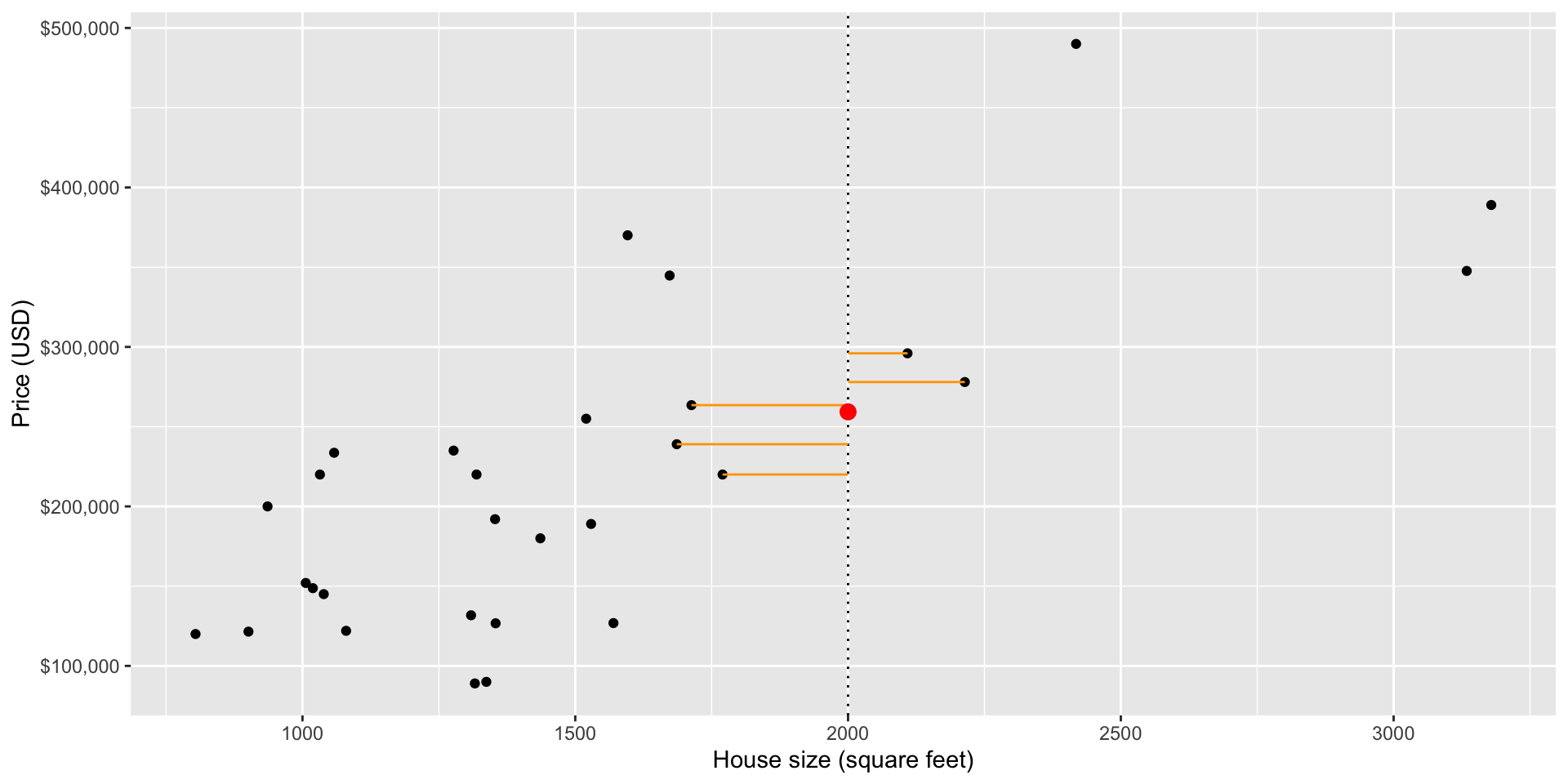
Prediction

• We would employ intuition from the classification chapter, and use the neighboring points to the new point of interest to suggest/predict what its sale price might be.

The predicted price for a house with 2000 square footage, is the average price of it’s five nearest neighbours:

(prediction <- nearest_neighbors |>
  summarise(predicted = mean(price)))

Predicted price

Code

small_plot + 
  geom_segment(data = nearest_neighbors, color = "orange",
               aes(x = sqft, xend = 2000, y = price, yend = price)) + 
  geom_point(data = data_frame(x = 2000, y = prediction$predicted), 
             aes(x, y), color = "red", size = 3)

so we can use this predicted price to inform our offer 2.593^{5}

Choosing K

• As with KNN classification, in KNN regression we still have the same question of how we best choose K, the number of nearest neighbours.

• Luckily for, the answer is the same: we use cross-validation to tune the model

• This will provide some guidance as to the optimal choice of our tuning parameter K

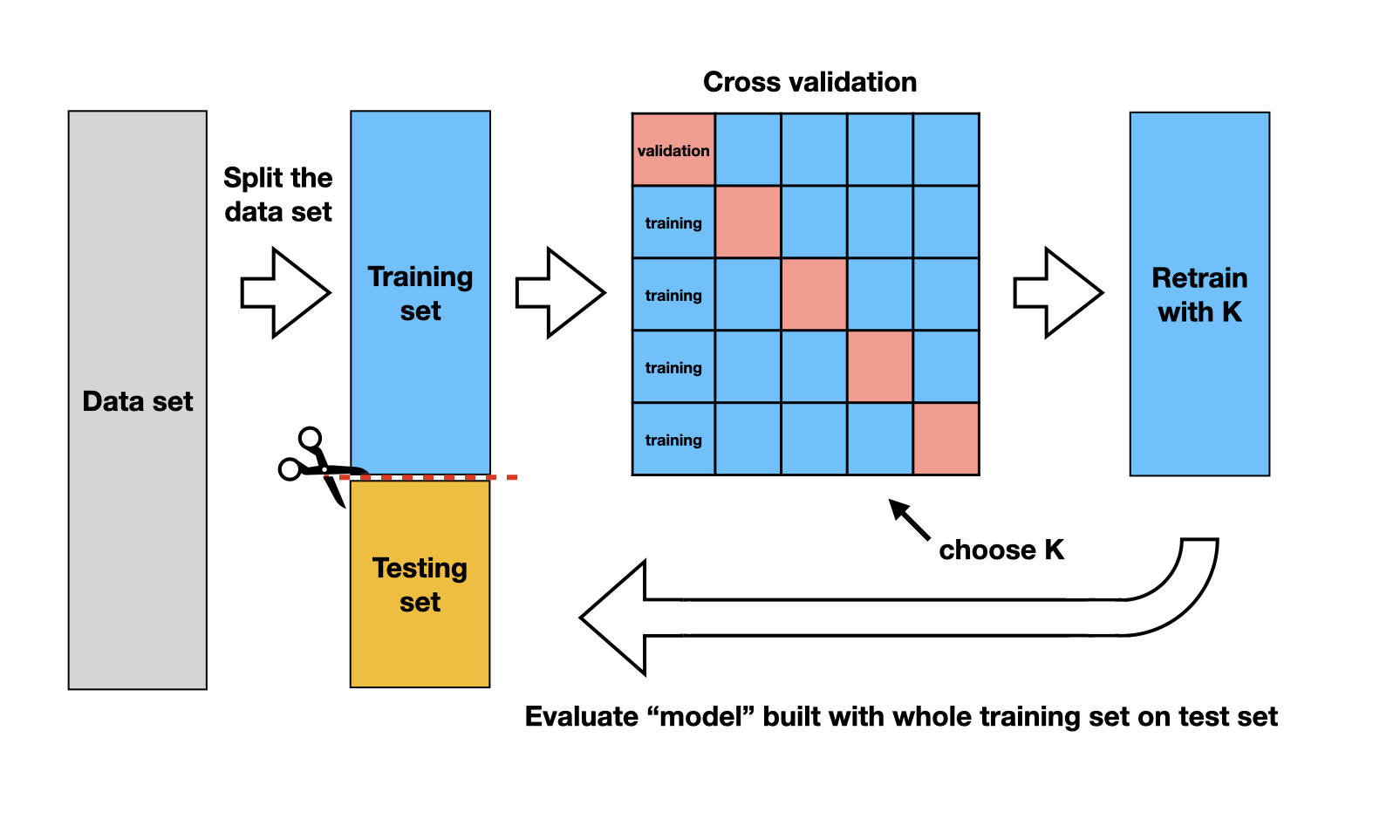
Steps for fitting the model

1. Split into training and test set
2. Preform cross validation to determine K
3. Retain the model with this chosen K
4. Evaluate how we did on the test set

Training/Test set

sacramento_split <- initial_split(sacramento, prop = 0.75, strata = price)
sacramento_train <- training(sacramento_split)
sacramento_test <- testing(sacramento_split)

The above splits the data frame into 75% training and 25% test.

• Numeric strata are binned into quartiles¹
• Hence there will be roughly the same proportion of houses in each of these four bins in both the training and testing set.

1. Quartiles are statistical measures that divide a dataset into four equal parts, with each part containing approximately 25% of the data points.

Cross Validation

• Next, we’ll use cross-validation to choose K

• In KNN classification, we used accuracy to see how well our predictions matched the true labels.

• We cannot use the same metric in the regression setting, since our predictions will almost never exactly match the true response variable values.

• Therefore in the context of KNN regression we will need a different metric …

RMPSE

For KNN regression the evaluation metric that we will use to quantify the performance of the model is the root mean square prediction error (RMSPE) given by:

\[\begin{equation} \text{RMSPE} = \sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}(y_i - \hat{y}_i)^2} \end{equation}\]

• \(n\) is the number of observations,

• \(y_i\) is the observed value for the \(i^{th}\) observation, and

• \(\hat y_i\) is the forecasted/predicted value for the \(i^{th}\) observation.

Note that this is computed over unseen data points (either our test or validation set)

• In words: - Calculate the squared difference between the predicted and true response for each observation in our test (or validation) set, compute the average, and then take the square root.
• the squared difference between the predicted and true response value for each observation in our test (or validation) set, compute the average, and then finally take the square root.
• why squared? since differences can be positive or negative,
• If the predictions are very close to the true values, then RMSPE will be small.
• otherwise then RMSPE will be quite large.
• In CV we choose the K that gives us the smallest RMSPE.

Comments

• If the predictions are very close to the true values, then RMSPE will be small.
• If, on the other-hand, the predictions are very different from the true values, then RMSPE will be quite large.
• When we use cross-validation, we will choose the K that gives us the smallest RMSPE.

• why squared? since differences can be positive or negative,

Note: Another common metric is mean squared error (MSE)
\[\text{MSE} = \frac{1}{n}\sum\limits_{i=1}^{n}(y_i - \hat{y}_i)^2\]

Terminology Alert

You textbook makes the distinction between calculating this metric on the training set, vs a testing/validation set (aka out-of-sample predictions)

Prediction error on the test/validation set: \[\begin{equation} \text{RMSPE} = \sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}(y_i - \hat{y}_i)^2} \end{equation}\] where \(\hat y_i\) our out-of-sample predictions.

The prediction error on the training set: \[\begin{equation} \text{RMSPE} = \sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}(y_i - \hat{y}_i)^2} \end{equation}\] where \(\hat y_i\) our in-sample predictions.

Warning

Many places use RMSE for both, and rely on context to denote which data the root mean squared error is being calculated on.

Recipe

First, we will create a recipe for preprocessing our data.

sacr_recipe <- recipe(price ~ sqft, data = sacramento_train) |>
  step_scale(all_predictors()) |>
  step_center(all_predictors())

This will normalize our predictor to have a mean of 0 and standard deviation of 1.

Note

Note that we include standardization in our preprocessing to build good habits, but since we only have one predictor, it is technically not necessary; there is no risk of comparing two predictors of different scales.

Model Specification

Next we create a model specification for K-nearest neighbors regression.

sacr_spec <- nearest_neighbor(weight_func = "rectangular", 
                              neighbors = tune()) |>
  set_engine("kknn") |>
  set_mode("regression")

Note that we use set_mode("regression") now in the model specification to denote a regression problem, as opposed to the classification problem.

parsnips 3 categories for model:

• type: the structural aspect of the model,

• mode: the modeling goal: regression or classification¹

• engine the estimation method and the implementation.

1. as per the calculated Euclidean distance; recall it is advisable to scale your data

Cross Validation Workflow

Then we create a cross-validation object (we will use 5-fold), and put the recipe (sacr_recipe) and model specification (sacr_spec) together using workflow().

sacr_vfold <- vfold_cv(sacramento_train, v = 5, strata = price)

sacr_wkflw <- workflow() |>
  add_recipe(sacr_recipe) |>
  add_model(sacr_spec)

sacr_wkflw

Cross Validation Workflow

══ Workflow ════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: nearest_neighbor()

── Preprocessor ────────────────────────────────────────────────────────────────
2 Recipe Steps

• step_scale()
• step_center()

── Model ───────────────────────────────────────────────────────────────────────
K-Nearest Neighbor Model Specification (regression)

Main Arguments:
  neighbors = tune()
  weight_func = rectangular

Computational engine: kknn 

CV grid

• Next we run CV for a grid of candidate values for K
• While K could be any integer from 1 to 698 (number of observations in our training set), we will thin out this vector and try every third number ranging from 1 to 200.

gridvals <- tibble(neighbors = seq(from = 1, to = 200, by = 3))

sacr_results <- sacr_wkflw |>
  tune_grid(resamples = sacr_vfold, grid = gridvals) |>
  collect_metrics() |>
  filter(.metric == "rmse")

# show the results
sacr_results

The following code tunes the model and returns the RMSPE for each number of neighbors. In the output of the sacr_results results data frame, we see that the neighbors variable contains the value of
K , the mean (mean) contains the value of the RMSPE estimated via cross-validation, and the standard error (std_err) contains a value corresponding to a measure of how uncertain we are in the mean value. A detailed treatment of this is beyond the scope of this chapter; but roughly, if your estimated mean is 100,000 and standard error is 1,000, you can expect the true RMSPE to be somewhere roughly between 99,000 and 101,000 (although it may fall outside this range). You may ignore the other columns in the metrics data frame, as they do not provide any additional insight.

CV grid

CV plot

Code

rmspe_vs_k <- ggplot(sacr_results, aes(x = neighbors, y = mean)) +
  geom_point() +
  geom_line() +
  labs(x = "Number of Nearest Neighbors (K)", y = "RMSPE Estimate") 


rmspe_vs_k

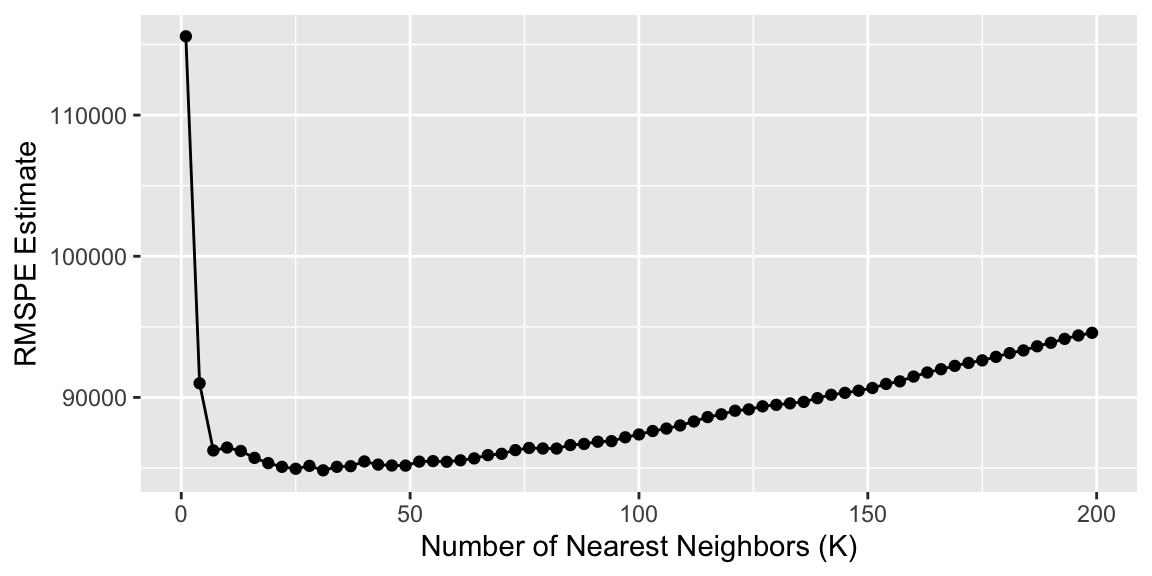
Best K

Since it’s a little bit hard to tell on the plot where the minimum lies, let’s find automate it:

# show only the row of minimum RMSPE
sacr_min <- sacr_results |>
  filter(mean == min(mean))

sacr_min

CV plot

Code

rmspe_vs_k + geom_vline(xintercept = sacr_min$neighbors, linetype = "dotted") +
  geom_text(aes(x = sacr_min$neighbors, y = 100000, label = paste("K =", sacr_min$neighbors)))

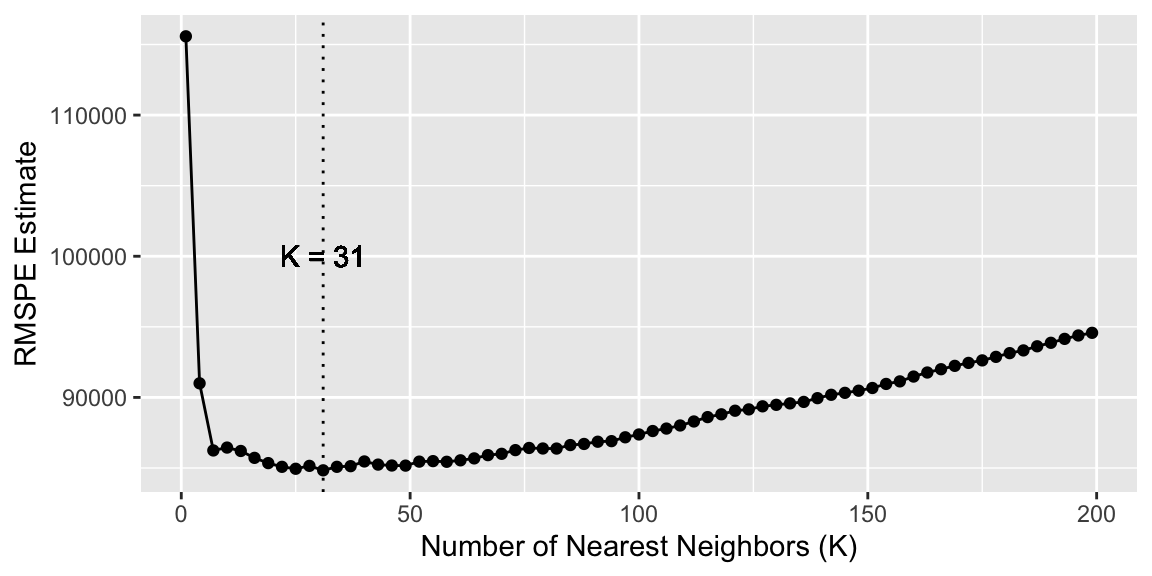
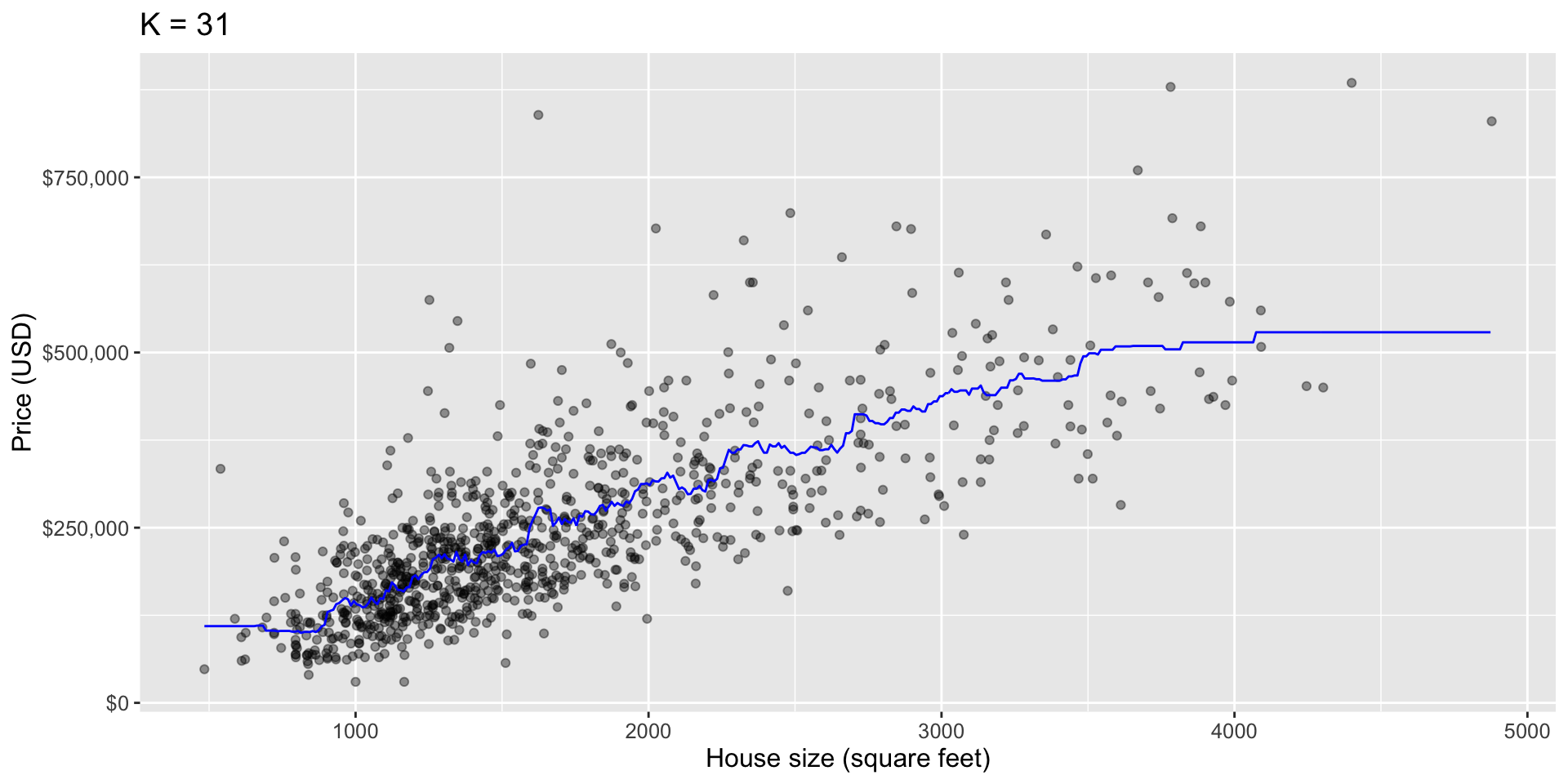
The smallest RMSPE occurs when K = 31

Bad Ks

• As in the classification setting, if we choose a K that is too small (e.g. K = 4) we would expect the error of our model to go up.

• Similarly, if we choose a value of K that is too big (e.g. K = 200) we would expect the error of our model to go up.

• Let’s visualizes the effect of different settings of the number of neighbors on the regression model …

K too small

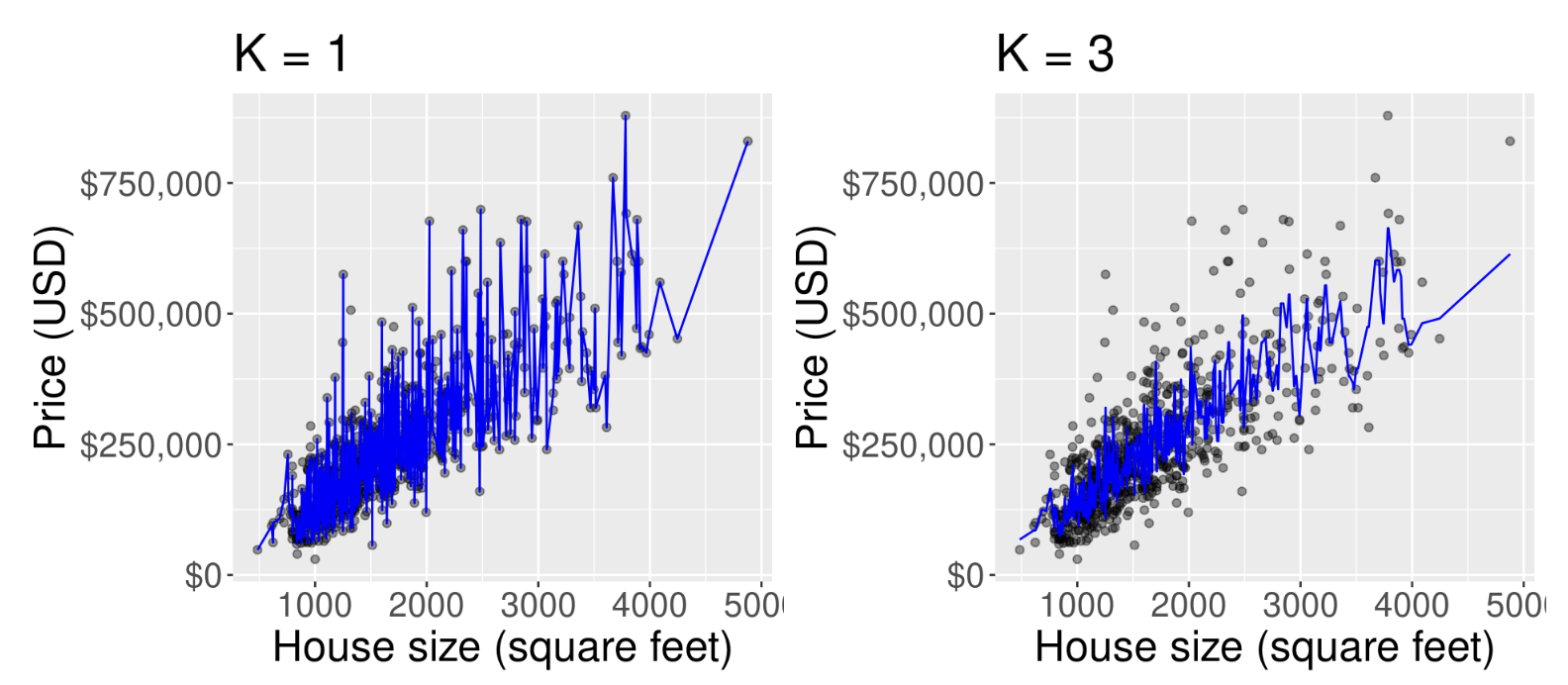
The predicted values for house sale price for a KNN regression model fitted on the training data with K = 1 (left) and K = 3 (right).

• When K = 1, the blue line runs perfectly through (almost) all of our training observations.
• This happens because our predicted values for a given region (typically) depend on just a single observation
• When K = 1, the blue line is following the training data too closely as opposed to picking up on the general trend of this relationship.

Overfitting

• In general, when K is too small, the model captures the noise and random fluctuations in the training data, rather than the underlying patterns and trends.
• In other words, the line follows the training data too closely.
• This leads to poor predictive performance on new data because the model has essentially memorized the training data rather than learning the underlying relationships.
• This behavior—where the model fits the training data extremely closely but doesn’t generalize well to unseen or new data—is called overfitting

• If we used a different training data set of house prices and sizes from the Sacramento real estate market, we would end up with completely different predictions.
• In other words, the model is influenced too much by the data.
• if is picking up on the noise in this training set, as opposed to picking up on the general trend of this relationship, it will not make accurate predictions on new observations which, generally, will not have the same fluctuations as the original training data.

K too big

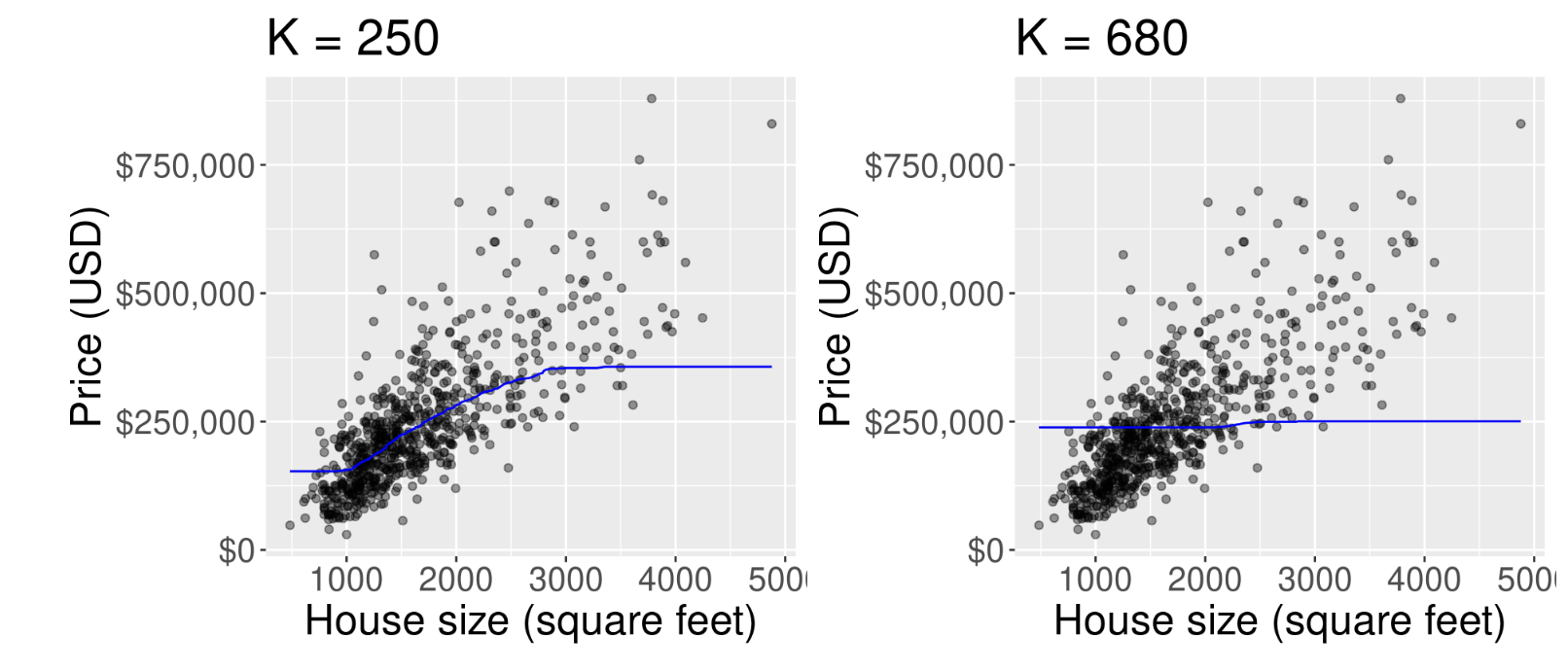
The predicted values for house sale price for a KNN regression model fitted on the training data with K = 250 (left) and K = 380 (right).

• blue line becomes extremely smooth, and actually becomes flat once K = \(n\)
• why? when K = \(n\) the prediction is just the mean of the house prices (completely ignoring the house size).
• the model is not influenced enough by the training data.

Underfitting

• In general, when K is too large, the model is not influenced enough by the training data!
• In other words this model is not flexible enough to capture the underlying patterns in the data
• This results in poor performance both on the training data and on new, unseen data.
• This behavior—when a model is too simplistic to capture the underlying patterns in the data—is called underfitting

• Underfitting is the opposite of overfitting and is another common issue in machine learning and statistical modeling.
• In underfitting, the model’s complexity is insufficient to represent the relationships in the data accurately.

Sweet spot

• Ideally, what we want is neither of the two situations discussed above. Instead, we would like a model that

  • follows the overall “trend” in the training data, so the model actually uses the training data to learn something useful, and
  • does not follow the noisy fluctuations, so that we can be confident that our model will transfer/generalize well to other new data.

We can see that other values for K achieves this goal \(\dots\)

Optimal K

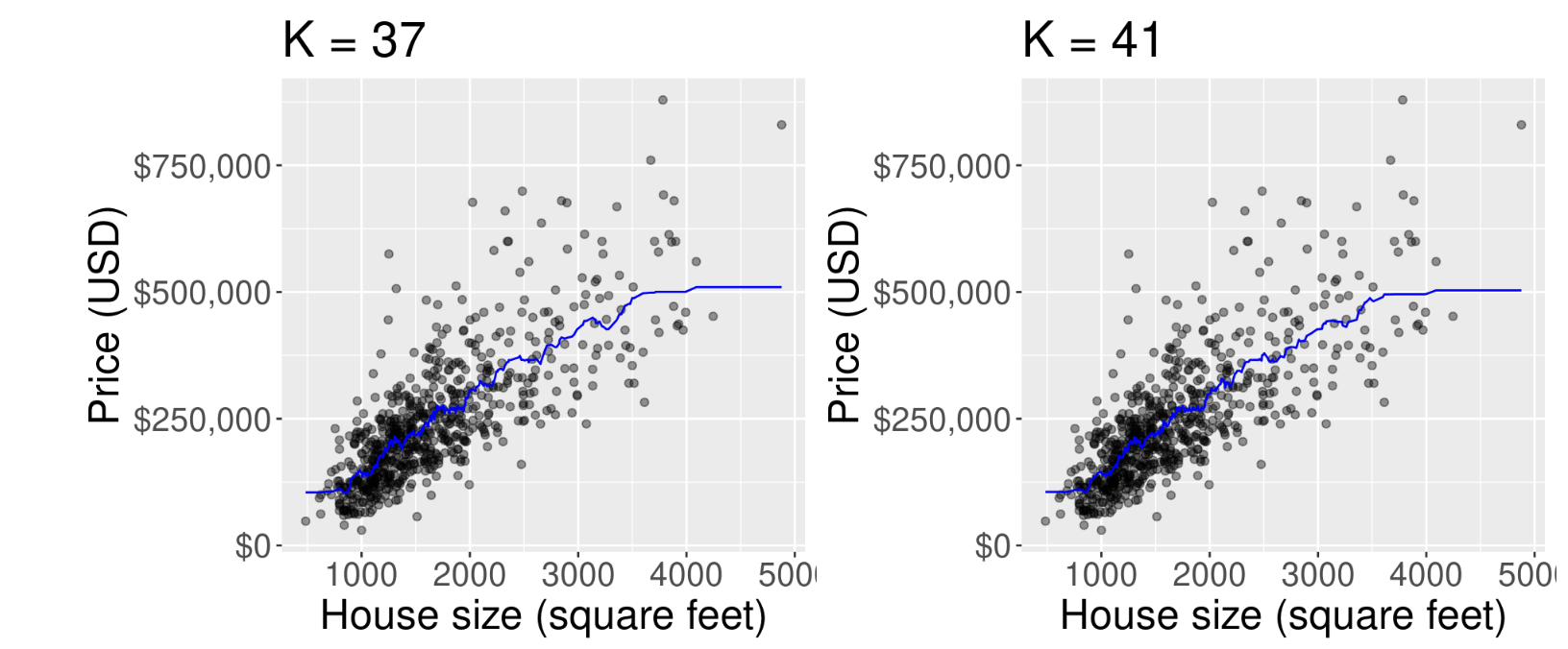
The predicted values for house sale price for a KNN regression model fitted on the training data with K = 37 (left) and K = 41 (right).

it follows the increasing trend of house price versus house size, but is not influenced too much by the idiosyncratic variations in price. All of this is similar to how the choice of K affects K-nearest neighbors classification, as discussed in the previous chapter.

Our best model

• Let’s explore the fit which our CV deemed best

• Note that our best K is slightly different than the textbook since we are not using the same seed!

• To do this, we will first re-train our KNN regression model on the entire training data set, using
  K= 31 neighbors.

Retraining the model

kmin <- sacr_min |> pull(neighbors)

sacr_spec <- nearest_neighbor(weight_func = "rectangular", 
                              neighbors = kmin) |>
  set_engine("kknn") |>
  set_mode("regression")

sacr_fit <- workflow() |>
  add_recipe(sacr_recipe) |>
  add_model(sacr_spec) |>
  fit(data = sacramento_train)

Evaluate our model on the test set

To quantify the performance of our fitted model we compute its RMSPE on the test data.

sacr_summary <- sacr_fit |>
  predict(sacramento_test) |>
  bind_cols(sacramento_test) |>
  metrics(truth = price, estimate = .pred) |>
  filter(.metric == 'rmse')

sacr_summary

Finally, we will assess how well our model might do at predicting on unseen data

Comment

• Our final model’s test error as assessed by RMSPE is $86813.53 (this measured in the same units as the response variable).
• In other words, on new observations, we expect the error in our prediction to be roughly $86813.53.
• In this application, this error is not prohibitively large, but it is not negligible either; $86813.53 might represent a substantial fraction of a home buyer’s budget.

• whether this value for RMSPE is good—i.e., whether an error of around $89,279 is acceptable—depends entirely on the application.
• and could make or break whether or not they could afford put an offer on a house.
• From one perspective, this is good news: this is about the same as the cross-validation RMSPE estimate of our tuned model (which was $85,227), so we can say that the model appears to generalize well to new data that it has never seen before.

we could possibly reduce this error by including more predictors (multivariate KNN)

Predictions of our fitted model

• The following code calculates the predictions that our final model makes across the range of house sizes we might encounter in the Sacramento area (roughly 500 to 5000 square feet).

• As a coding challenge, go through this code on your own time to reproduce the plot

Code

# range of plausible house sizes 
sqft_prediction_grid <- tibble(
    sqft = seq(
        from = sacramento |> select(sqft) |> min(),
        to = sacramento |> select(sqft) |> max(),
        by = 10
    )
)

# predicted price of these hypothetical houses
sacr_preds <- sacr_fit |>
  predict(sqft_prediction_grid) |>
  bind_cols(sqft_prediction_grid)

# scatter plot of price vs. square footage
plot_final <- ggplot(sacramento, aes(x = sqft, y = price)) +
  geom_point(alpha = 0.4) +
  # superimpose prediction line 
  geom_line(data = sacr_preds, 
            mapping = aes(x = sqft, y = .pred), 
            color = "blue") +
  xlab("House size (square feet)") +
  ylab("Price (USD)") +
  scale_y_continuous(labels = dollar_format()) +
  ggtitle(paste0("K = ", kmin)) + 
  theme(text = element_text(size = 12))

plot_final

Predictions of our fitted model

Predicted values of house price (blue line) for the final KNN regression model.

Multivariable KNN

• For both KNN classification and KNN regression we can use multiple predictors in our model.

• For instance, the number of bedrooms (beds) and bathrooms (baths) may prove to be useful predictors in determining the selling price (price).

• We can very easily adjust our code to include more than one predictor.

Warning

Warning

Having more predictors is not always better

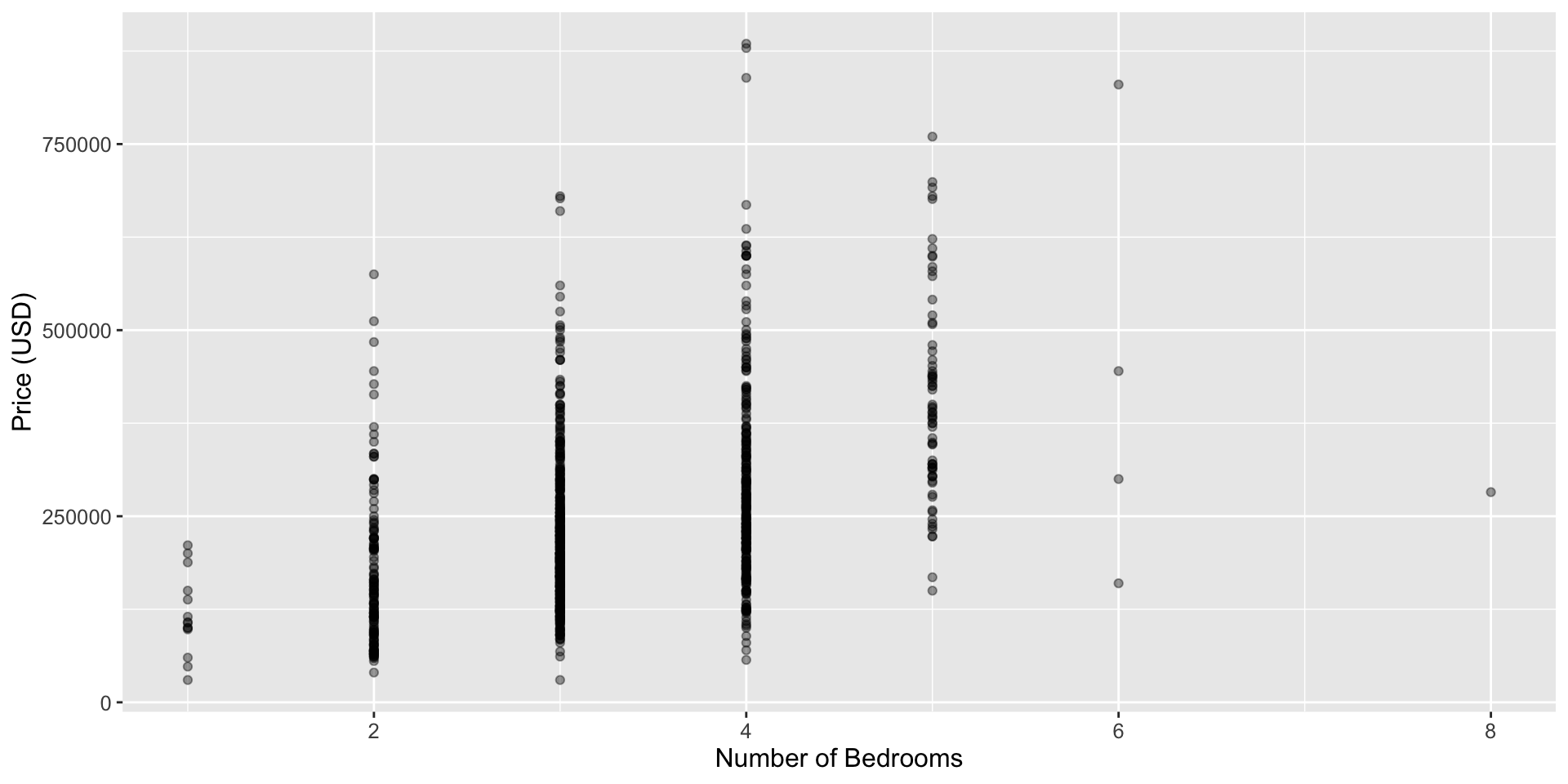
• To demo multivariate KNN we we will use house size (measured in square feet) as well as number of bedrooms as our predictors.
• If we want to compare this multivariable KNN regression model to the model with only a single predictor, then we can compare the accuracy estimated using only the training data via cross-validation.

EDA bedrooms

plot_beds <- sacramento |>
  ggplot(aes(x = beds, y = price)) +
  geom_point(alpha = 0.4) + 
  labs(x = 'Number of Bedrooms', y = 'Price (USD)') + 
  theme(text = element_text(size = 12))
plot_beds

• It is always a good practice to do exploratory data analysis, such as visualizing the data, before we start modeling the data.
• as the number of bedrooms increases, the house sale price tends to increase as well, but that the relationship is quite weak.

Recipe + Specfication

sacr_recipe <- recipe(price ~ sqft + beds, data = sacramento_train) |>
  step_scale(all_predictors()) |>
  step_center(all_predictors())
sacr_spec <- nearest_neighbor(weight_func = "rectangular", 
                              neighbors = tune()) |>
  set_engine("kknn") |>
  set_mode("regression")

CV for choosing K

gridvals <- tibble(neighbors = seq(1, 200))

sacr_multi <- workflow() |>
  add_recipe(sacr_recipe) |>
  add_model(sacr_spec) |>
  tune_grid(sacr_vfold, grid = gridvals) |>
  collect_metrics() |>
  filter(.metric == "rmse") |>
  filter(mean == min(mean))

sacr_k <- sacr_multi |> pull(neighbors)

sacr_multi

Multivariate KNN results

• Here we see that the smallest estimated RMSPE from cross-validation occurs when K = 10
• Looking back, the estimated cross-validation accuracy for the single-predictor model was $86813.53,227.
• The estimated cross-validation accuracy for the multivariable model is $85034.51.
• Thus in this case, we did not improve the model by a large amount by adding this additional predictor.