Lecture 11: Cross Validation

DATA 101: Making Prediction with Data

Dr. Irene Vrbik

University of British Columbia Okanagan

Introduction

• In the last lecture we saw how we could fit the KNN classification models using tidymodels.
• Recall: tidymodels is an R package and framework for modeling that follows the principles of the tidyverse.
• In the upcoming lectures we will continue to work with tidymodels for evaluation and tuning

tidymodels packages

recipes: tidy interface for data pre-processing

parnips: tidy interface for fitting models

rsample: tidy interface for data splitting and resampling

yardstick tidy interface for validating models

just like we’re using tidyverse to do out data wrangling and visualization, we use tidymodels to do our modeling.

1. pre-process
2. train
3. validate

also workflows workflows makes this easier by combining or bundling these pre-processing, modeling, and post-processing requests together

we won’t focus too much on which package is doing what

Why tidymodels?

• R is open source – made by different people and using different principles, everything has a slightly different interface, and trying to keep everything in line can be frustrating
• tidymodels offers a consistent interface with many other R packages who do the work of fitting the models

• no need to look at a specify package which may specify things in a different format than another package

Steps of tidymodels

1. Build and fit a model
2. Preprocess your data with recipes
3. Evaluate your model with resamples
4. Tune model parameters
5. A predictive modeling case study

https://www.tidymodels.org/start/: Learn what you need to know to start using tidymodels in 5 articles. Dive deeper at: https://www.tidymodels.org/learn/

Steps of tidymodels

1. Preprocess your data with recipes
2. Build and fit a model
3. Evaluate your model with resamples
4. Tune model parameters
5. A predictive modeling case study

We’ll go through building the model first but typically the pre-processing happens before training your model

• recipes is designed to help you preprocess your data

https://www.tidymodels.org/start/: Learn what you need to know to start using tidymodels in 5 articles. Dive deeper at: https://www.tidymodels.org/learn/

Cancer Data

Let’s continue with our example from last class:

library(tidyverse)
library(tidymodels)
cancer <- read_csv("data/clean-wdbc-data.csv")
cancer <- cancer |> mutate(Class = as_factor(Class)) |>
  mutate(Class = fct_recode(Class, "Malignant" = "M", "Benign" = "B"))

Recall that this is a classification problem in which we wish to classify tumors as either being malignant or benign.

malignant = cancerous

benign = non-canerous

Scatterplot

Code

# create scatter plot of tumor cell concavity versus smoothness,
# labeling the points be diagnosis class
perim_concav <- cancer |>
  ggplot(aes(x = Smoothness, y = Concavity, color = Class)) +
  geom_point(alpha = 0.5) +
  labs(color = "Diagnosis") +
  scale_color_manual(values = c("orange2", "steelblue2")) + 
  theme(text = element_text(size = 12))

perim_concav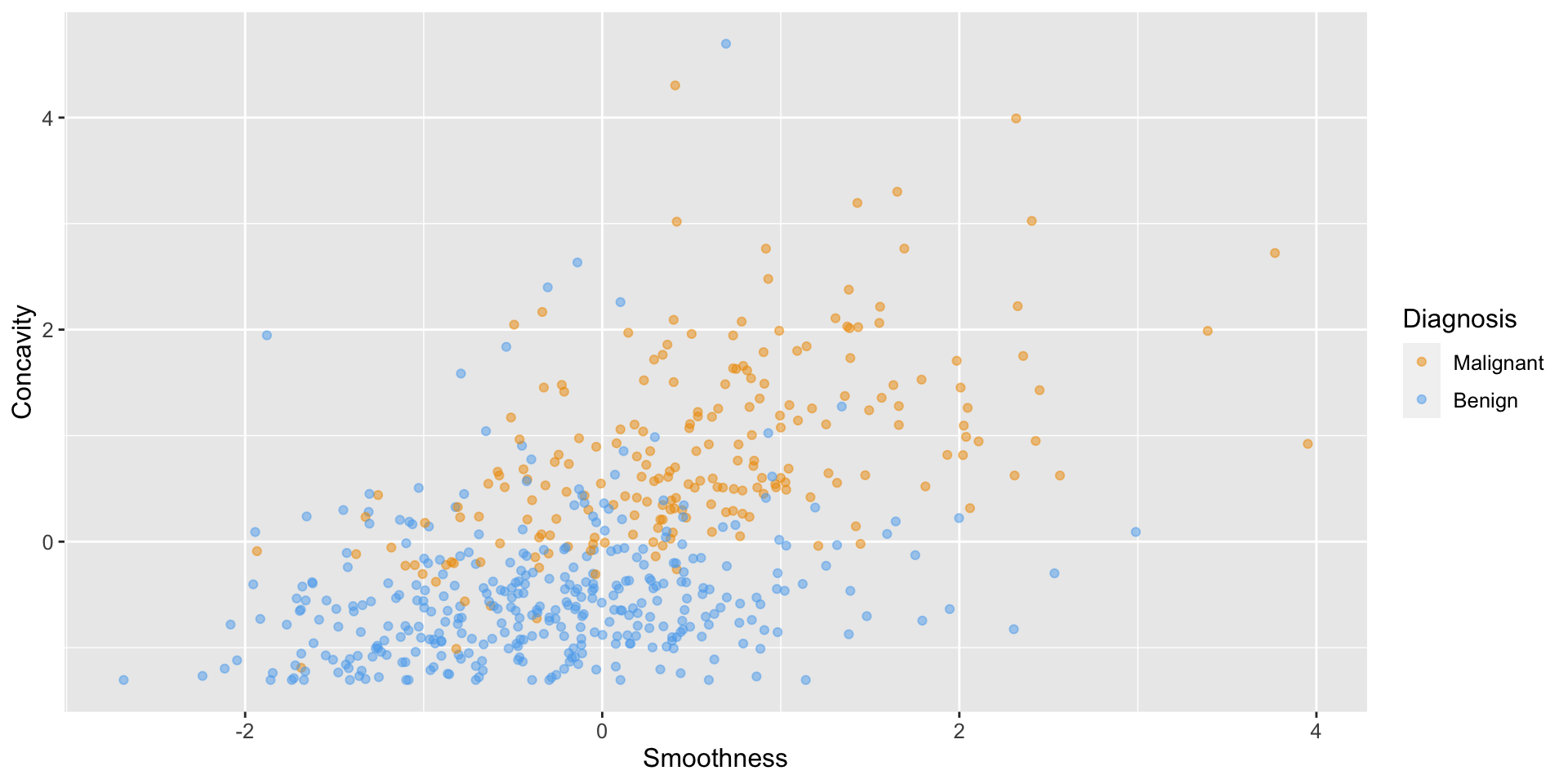

whhile there are 11 predictors to choose from, we’re investigating concavity and permiter

Create Training/Test set

Before we do anything, we want to split our data into a training and testing test…

set.seed(4297026)
cancer_split <- initial_split(cancer, prop = 0.75, strata = Class)
cancer_train <- training(cancer_split)
cancer_test <- testing(cancer_split) 

• initial_split creates the training and testing sets.
• specify that prop = 0.75 so that 75% of our original data set ends up in the training set.
• strata argument to the categorical label variable (here, Class) to ensure that the training and testing subsets contain the right proportions of each category of observation.
• The training and testing functions extract the training and testing data sets into two separate data frames.
• Note that the initial_split function uses randomness, but since we set the seed earlier in the chapter, the split will be reproducible.

1. Build a model

Parsnip categorizes models by:

• type: the structural aspect of the model,

• mode: the modeling goal: regression or classification¹

• engine: the estimation method and the implementation.

For example, for linear regression, one engine is "lm" which uses ordinary least squares analysis via the lm() function. Another engine is "stan" which uses the Stan infrastructure to estimate parameters using Bayes rule.

show_engines("nearest_neighbor")

1. Some models have methods for both models (e.g. nearest neighbors) while others have only a single mode (e.g. logistic regression).

Model type

nearest_neighbor()

K-Nearest Neighbor Model Specification (unknown mode)

Computational engine: kknn 

• To predict the label of a new observation (here, classify it as either benign or malignant), we will used the K-nearest neighbors (KNN) classification algorithm.

• The model type is related to the structural aspect of the model. For example, the model type linear_reg represents linear models (slopes and intercepts) that model a numeric outcome. Other model types in the package are nearest_neighbor, decision_tree, and more.

• find K nearest neighbours, and then uses their diagnoses to make a prediction for the new observation’s diagnosis.

• That is pretty underwhelming since, on its own, it doesn’t really do much.

• However, now that the type of model has been specified, we can think about a method for fitting or training the model, the model engine.

show_engines("nearest_neighbor")

Model engine

nearest_neighbor(neighbors = 6) |>
  set_engine("kknn") 

K-Nearest Neighbor Model Specification (unknown mode)

Main Arguments:
  neighbors = 6

Computational engine: kknn 

The computation engine is a combination of the estimation method and the implementation. For example, for linear regression, one engine is “lm” which uses ordinary least squares analysis via the lm() function. Another engine is “stan” which uses the Stan infrastructure to estimate parameters using Bayes rule.

Unlike last class, this version of nearest_neighbor does not specify a particular weighting function, so it uses the default weighting function, which is often "rectangular" by default (same as last class). We will use 6 nearest neighbours instead of 5 to avoid confusion with 5-fold cross-validation.

Model mode

knn_spec <- nearest_neighbor(weight_func = "rectangular",
                             neighbors = 6) |>
  set_engine("kknn") |>
  set_mode("classification")

The mode is related to the modeling goal. Currently the two modes in the package are regression and classification. Some models have methods for both models (e.g. nearest neighbors) while others have only a single mode (e.g. logistic regression).

Jump to Parameter value selection

Fit the model

Now we train the classifier using the predictors Perimeter and Concavity using the fit() function

knn_spec |> fit(Class ~ Perimeter + Concavity, data = cancer_train) 

parsnip model object


Call:
kknn::train.kknn(formula = Class ~ Perimeter + Concavity, data = data,     ks = min_rows(6, data, 5), kernel = ~"rectangular")

Type of response variable: nominal
Minimal misclassification: 0.07042254
Best kernel: rectangular
Best k: 6

• fit() is from the parsnip pacakge.
• these objects are imported from other packages.
• knn_spec object represents the KNN model that you’ve defined. It encapsulates the model specification, engine, and data used for training.
• You can use this object to make predictions, evaluate the model’s performance, or further customize the modeling process.
• notice the training set

More than 2 predictors

knn_spec |> fit(Class ~ ., data = cancer_train) 

If we wanted to use every variable in (exepect Class) as a predictor in the model, we could use a convenient shorthand syntax above which is the same as:

knn_spec |> 
  fit(Class ~  ID + Radius + Texture + Perimeter + Area 
      + Smoothness + Compactness + Concavity + Concave_points 
      + Symmetry + Fractal_dimension, data = cancer_train) 

2. Pre-process

The recipes package which is designed to help you preprocess your data before training your model. Examples include:

• converting categorical predictors to indicator variables (also known as dummy variables),
• transforming data to be on a different scale (e.g., taking the logarithm of a variable),
• extracting key features from raw variables (e.g., getting the day of the week out of a date variable),

• can transform whole groups of predictors together,

Normalizing

Remember in our discussion of KNN we said it was useful to normalize our data before fitting?

cancer_recipe <- recipe(Class ~ Smoothness + Concavity, data = cancer_train) |>
  step_scale(all_predictors()) |>
  step_center(all_predictors())

The above will normalize numeric data to have a standard deviation of one a mean of zero.

Now let’s refit the model

As we mentioned in the last chapter,
K -nearest neighbors is sensitive to the scale of the predictors, so we should perform some preprocessing to standardize them. An additional consideration we need to take when doing this is that we should create the standardization preprocessor using only the training data. This ensures that our test data does not influence any aspect of our model training. Once we have created the standardization preprocessor, we can then apply it separately to both the training and test data sets.

step_center = normalize numeric data to have a mean of zero.

Workflow

knn_wflow <- workflow() |>
  add_recipe(cancer_recipe) |> # pre-processing
  add_model(knn_spec)          # model specification (build)

knn_fit <- knn_wflow |> fit(data = cancer_train)     

• without workflow we wouldn’t
• Note that we do not need to specify the formula again in fit since it has been specified in the recipe.
• knn_fit encapsulates the final trained model along with: model specification, engine, and data used for training.
• notice how we saved everything to one object: pre-processing, model spec and fit

Prediction

Now that we have a fitted KNN model, we can use it to predict the class labels for our test set.

predict(knn_fit, cancer_test) 

# A tibble: 143 × 1
   .pred_class
   <fct>      
 1 Benign     
 2 Malignant  
 3 Malignant  
 4 Benign     
 5 Malignant  
 6 Malignant  
 7 Malignant  
 8 Benign     
 9 Malignant  
10 Malignant  
# ℹ 133 more rows

Comment

• To assess our model we will need to compare the true class of the patients in the test set (cancer_test$Class) with the predict class we just outputted on the previous slide.

• To facilitate these comparison let’s save this information to new data frame

cancer_test_predictions <- predict(knn_fit, cancer_test) |>
  bind_cols(cancer_test)
cancer_test_predictions

use bind_cols to combine the column of predictions to the original test data

Comment

# A tibble: 143 × 13
   .pred_class       ID Class       Radius Texture Perimeter    Area Smoothness
   <fct>          <dbl> <fct>        <dbl>   <dbl>     <dbl>   <dbl>      <dbl>
 1 Benign        846226 Malignant  0.971     0.694    1.32    0.793     -1.26  
 2 Malignant   84799002 Malignant  0.246     1.86     0.501   0.110      1.55  
 3 Malignant     852763 Malignant  0.279     1.23     0.451   0.0287     0.882 
 4 Benign        852781 Malignant  1.04      0.258    0.971   0.918      0.0627
 5 Malignant     855563 Malignant -0.710     1.57    -0.596  -0.644      2.56  
 6 Malignant   85638502 Malignant -0.00811   0.685   -0.0524 -0.246      0.785 
 7 Malignant     857155 Benign    -0.519    -0.810   -0.517  -0.523      0.746 
 8 Benign        857392 Malignant  0.896    -0.252    0.828   0.774     -0.191 
 9 Malignant     857793 Malignant  0.331     0.817    0.251   0.184      0.194 
10 Malignant     859471 Benign    -1.23     -0.493   -1.24   -0.976      0.693 
# ℹ 133 more rows
# ℹ 5 more variables: Compactness <dbl>, Concavity <dbl>, Concave_points <dbl>,
#   Symmetry <dbl>, Fractal_dimension <dbl>

Evaluate performance

Finally, we can assess our classifier’s performance. First, we will examine accuracy. To do this we use the metrics function from tidymodels, specifying the truth and estimate arguments:

cancer_test_predictions |>
  metrics(truth = Class, estimate = .pred_class) |>
  filter(.metric == "accuracy")

# A tibble: 1 × 3
  .metric  .estimator .estimate
  <chr>    <chr>          <dbl>
1 accuracy binary         0.846

• In the metrics data frame, we filtered the .metric column since we are interested in the accuracy row.
• Other entries involve other metrics that are beyond the scope of this course
• Looking at the value of the .estimate variable shows that the estimated accuracy of the classifier on the test data was 84%.

Confusion Matrix

We can also look at the confusion matrix using conf_mat:

confusion <- cancer_test_predictions |>
             conf_mat(truth = Class, estimate = .pred_class)
confusion

           Truth
Prediction  Malignant Benign
  Malignant        41     10
  Benign           12     80

• how many false positive (predicted Malignant but actually benign) = 10
• how many false negatives (predicted benign but actually malignant) = 12
• how many correct predictions? 41 + 80 = 121

Other metrics

conf_mat = confusion[[1]]
(accuracy <- sum(diag(conf_mat)) / sum(conf_mat))
(recall <- conf_mat[2, 2] / sum(conf_mat[2, ]))
(precision <- conf_mat[2, 2] / sum(conf_mat[, 2]))

[1] 0.8461538
[1] 0.8695652
[1] 0.8888889

\[\begin{align} \text{accuracy} &= \frac{\text{number of correct predictions}}{\text{total number of predictions}}\\ \text{recall} &= \frac{\text{number of correct positive predictions}}{\text{total number of positive test set observations}}\\ \text{precision} &= \frac{\text{number of correct positive predictions}}{\text{total number of positive predictions}} \end{align}\]

• In this context, we need the classifier to have a high recall, i.e., we want our model to be very good at identifying malignant tumors.
• On the flip sidie, it might be less bad for the classifier to guess “malignant” when the true class is “benign” (a false positive), as the patient will then likely see a doctor who can provide an expert diagnosis.

Tuning Parameters

• The vast majority of predictive models in statistics and machine learning have tuning parameters.
• A tuning parameter (or hyperparamter) is a number you have to pick in advance that determines some aspect of how the model behaves.
• For the KNN classification algorithm, K, the value that determines how many neighbors participate in the class vote, is a tuning parameter.
• By picking different values of K, we create different classifiers that make different predictions.

Tuning the Classifier

• “Tuning a model”, refers to the process of adjusting the hyperparameters of a machine learning algorithm to optimize its performance on a specific task or dataset.

• The goal of tuning a model is to find the best set of hyperparameter values that result in a model that generalizes well to unseen data, provides better accuracy¹, and is well-suited to the specific problem at hand.

• In our example tuning the model equates to how we pick the best value of K

• we will focus on maximizing the accuracy of the classifier.
• could have just as easily used recall
• we will see that the regression problem uses another measure

1. or other performance metrics

Unseen data

• The first step in choosing the parameter K is to be able to evaluate each classifier¹
• The “best” classifier, would ideally, be the one which gets the accuracy on data it hasn’t seen yet.

• Problem: We cannot use our test data set in the process of building our model 🤔

• Solution: Cross-validation!

• Ideally, we want somehow to maximize the accuracy of our classifier on data it hasn’t seen yet.
• we will cover the details of this procedure, as well as how to use it to help you pick a good parameter value for your classifier.
• use one to train the model, and then use the other to evaluate it.
• Cross-validation (CV) is a technique commonly used in machine learning and statistics to estimate the model’s performance with different hyperparameter combinations

1. examples of classifiers: KNN with \(k=1\) , KNN with \(k=2\), \(\dots\), KNN with \(k = n\)

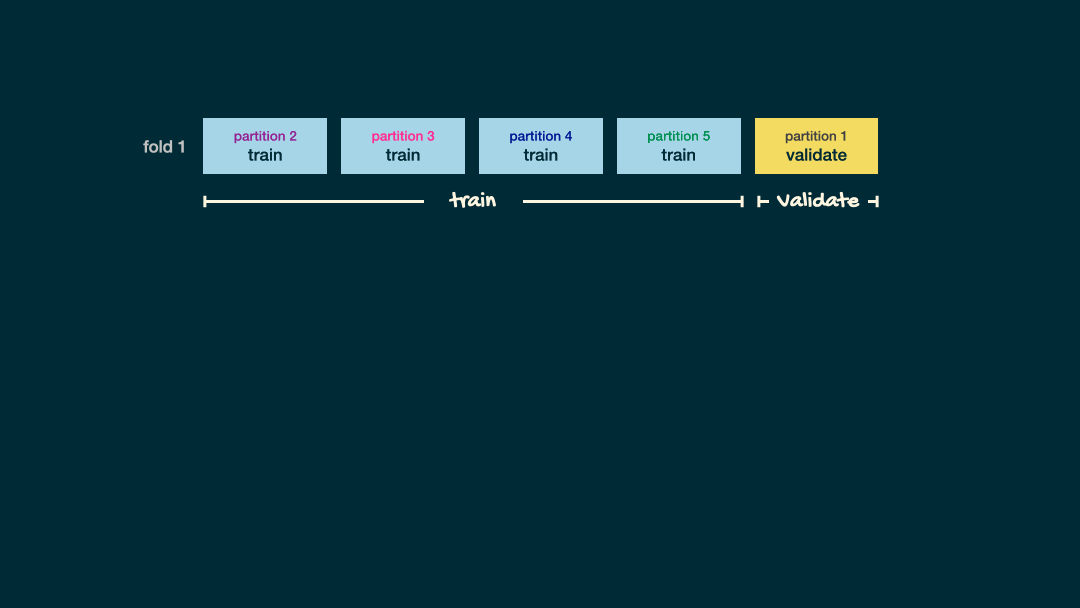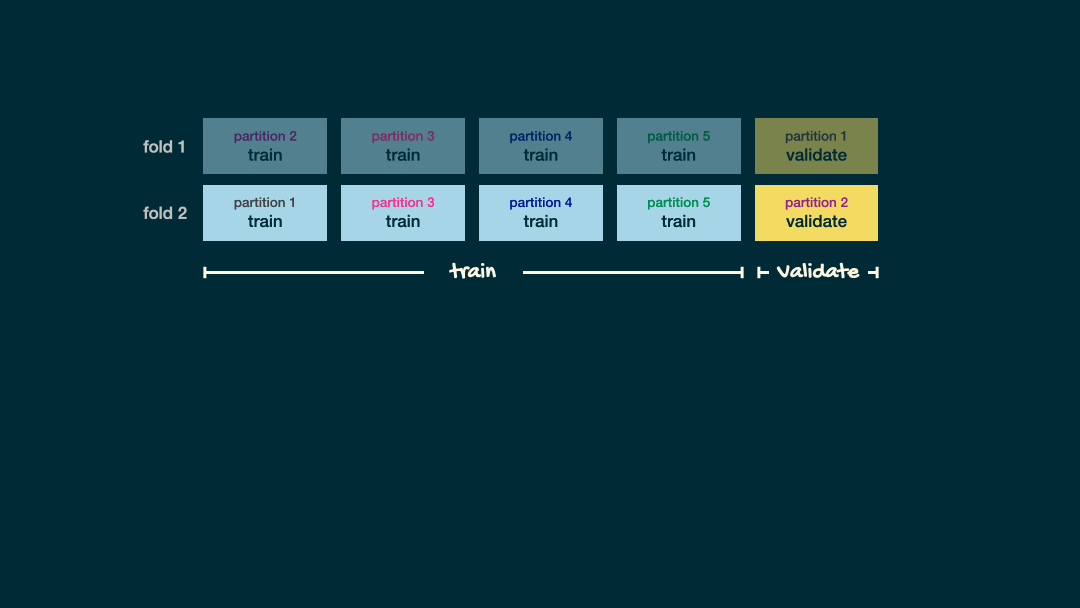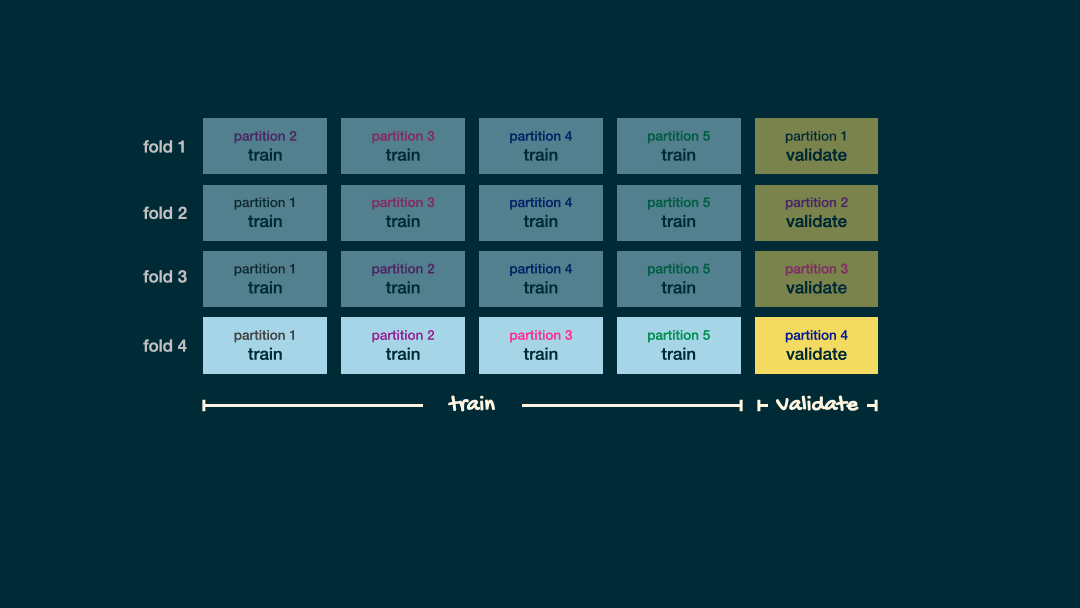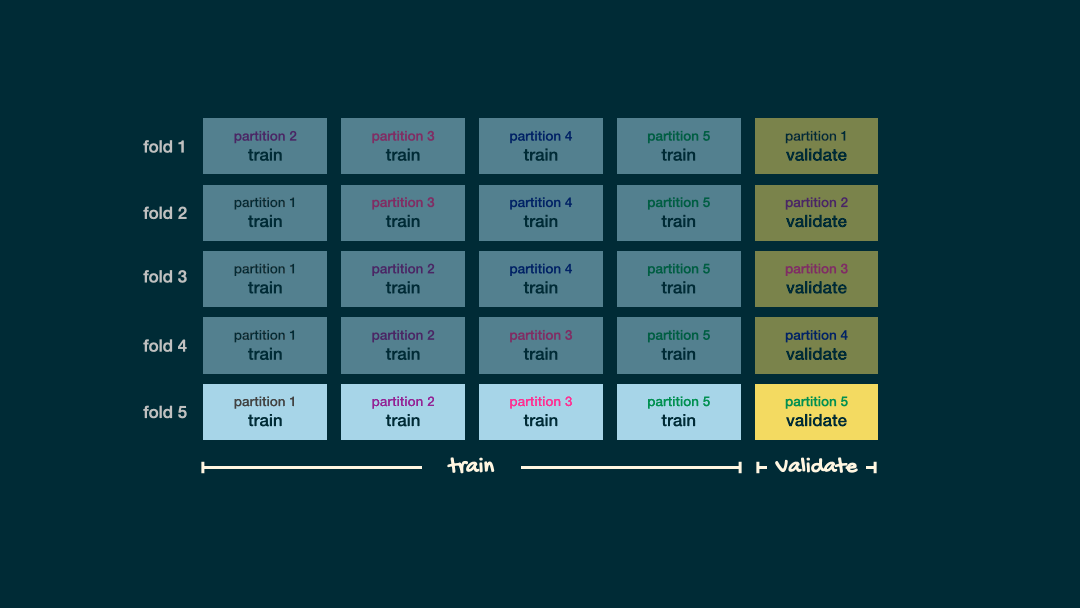
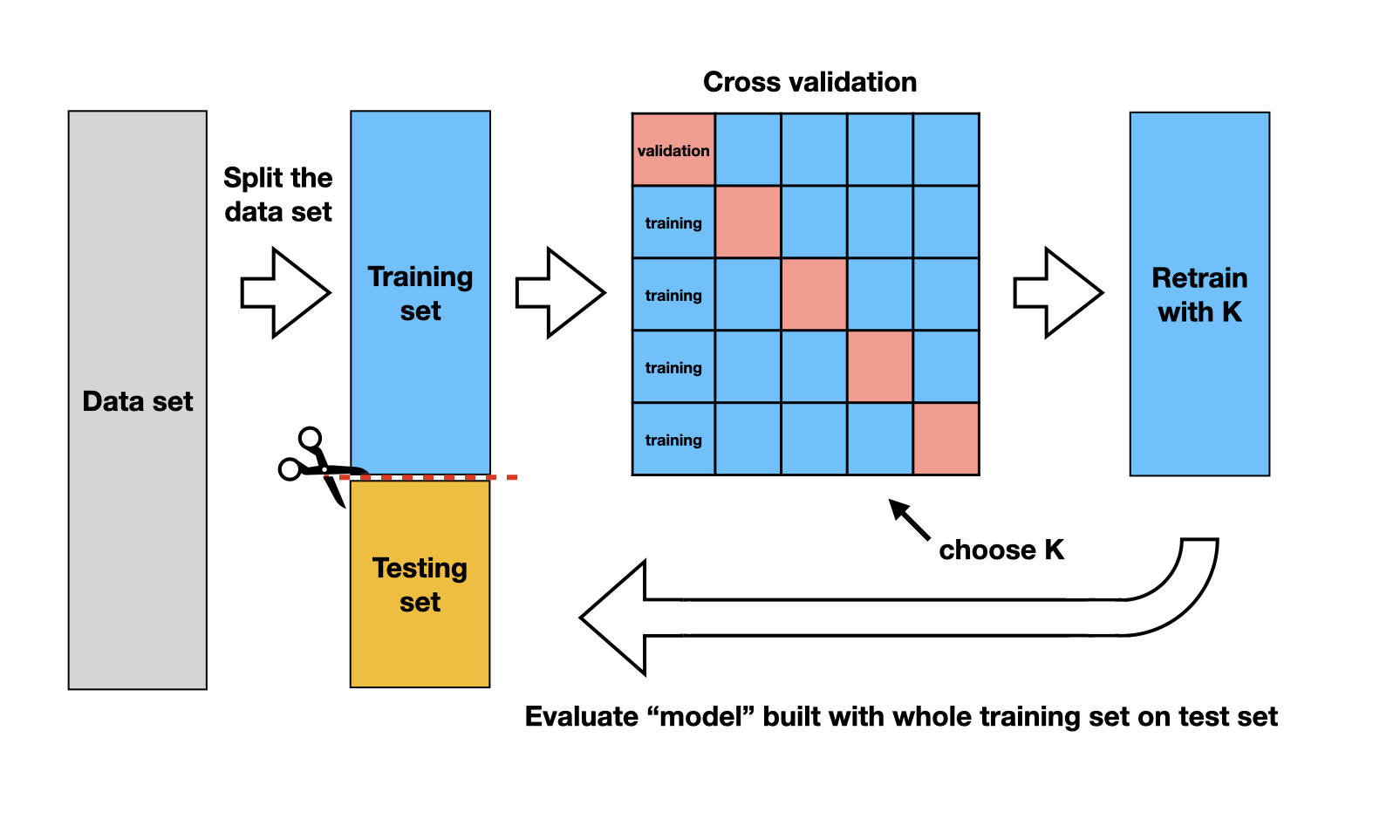
Cross-Validation

V-fold Cross-validation (CV) uses the same trick did before when evaluating our classifier, that is we will “hide” some data during the fitting process

• For example, 5-fold CV involves splitting the training data into five subsets
• Each subset will have a turn as the validation set
• That is, we will have 5 validation sets evaluating the five different fits (based five different subsets).
• We then aggregating the results to estimate how well the model is perform for that value of the hyperparameter

• In practice 5-fold and 10-fold cross validation is quite common.

• special case is leave one out cross validation in which we have \(n\)-folds

Cross-validation schematic

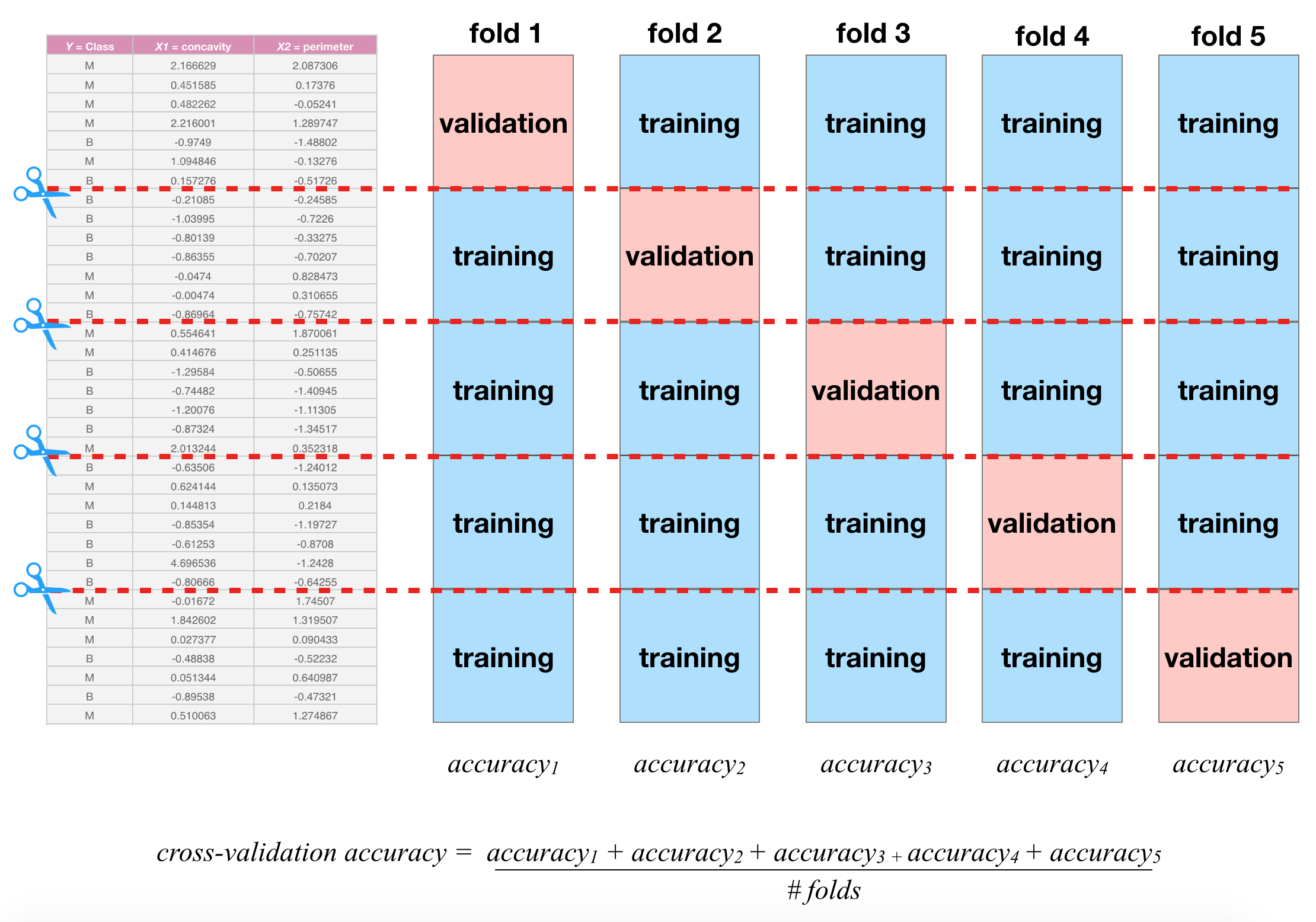
Depiction of 5-fold cross validation. Note that the data would be shuffled before creating these folds. Source Sec 6.6.1

One of these for each of our classifiers, KKN-1, KKN-2, … KNN-n

why multiple splits?

• If we just split our overall training data once, our best parameter choice will depend strongly on whatever data was lucky enough to end up in the validation set.

• Using multiple different train/validation splits, will give a better estimate of accuracy, which will lead to a better choice of the number of neighbors K for the overall set of training data.

Steps for tuning a model

1. Define a range or a set of possible values for the hyperparameter(s).
2. Select an evaluation metric that quantifies the performance of the model (e.g. accuracy)
3. Use cross-validation to estimate the model’s performance with different hyperparameter combinations.
4. Select the hyperparameter value(s) that result in the best model performance according to the chosen evaluation metric.

Visual example

For each of your potentail values of your hyperparameter you fit V models and calculated the CV-accuracy

KNN with \(k\) = 1

KNN with \(k\) = 2

KNN with \(k\) = 3

\(\dots\)

KNN with \(k\) = 424

KNN with \(k\) = 425

KNN with \(k\) = 426

for each of your potentail values of your hyperparameter you fit V models.

Visual example

The model which produces the best CV-accuracy is deemed the “best” model.

KNN with \(k\) = 1, CV-accuracy = 0.7

KNN with \(k\) = 2, CV-accuracy = 0.68

KNN with \(k\) = 3, CV-accuracy = 0.72

\(\dots\)

KNN with \(k\) = 424, CV-accuracy = 0.63

KNN with \(k\) = 425, CV-accuracy = 0.55

KNN with \(k\) = 426, CV-accuracy = 0.51

CV in R

To perform 5-fold CV with tidymodels, we use : vfold_cv.

set.seed(345)
(cancer_vfold <- vfold_cv(cancer_train, v = 5, strata = Class))

#  5-fold cross-validation using stratification 
# A tibble: 5 × 2
  splits           id   
  <list>           <chr>
1 <split [340/86]> Fold1
2 <split [340/86]> Fold2
3 <split [341/85]> Fold3
4 <split [341/85]> Fold4
5 <split [342/84]> Fold5

This function splits our training data into v folds automatically. We set the strata argument to the categorical label variable (here, Class) to ensure that the training and validation subsets contain the right proportions of each category of observation.

Adding to our workflow

We can reuse our previously created workflow, we use fit_resamples (instead of the fit function) for training.

# for the k = 5 KNN model
knn_cv_fit <- knn_wflow %>%
  fit_resamples(cancer_vfold)

knn_cv_fit

# Resampling results
# 5-fold cross-validation using stratification 
# A tibble: 5 × 4
  splits           id    .metrics         .notes          
  <list>           <chr> <list>           <list>          
1 <split [340/86]> Fold1 <tibble [2 × 4]> <tibble [0 × 3]>
2 <split [340/86]> Fold2 <tibble [2 × 4]> <tibble [0 × 3]>
3 <split [341/85]> Fold3 <tibble [2 × 4]> <tibble [0 × 3]>
4 <split [341/85]> Fold4 <tibble [2 × 4]> <tibble [0 × 3]>
5 <split [342/84]> Fold5 <tibble [2 × 4]> <tibble [0 × 3]>

• we use the fit_resamples function instead of the fit function for training.
• This runs cross-validation on each train/validation split.

Collect CV metrics

collect_metrics(knn_cv_fit) 

# A tibble: 2 × 6
  .metric  .estimator  mean     n std_err .config             
  <chr>    <chr>      <dbl> <int>   <dbl> <chr>               
1 accuracy binary     0.831     5 0.00482 Preprocessor1_Model1
2 roc_auc  binary     0.913     5 0.00621 Preprocessor1_Model1

• 0.831 is cross-validated estimate of accuracy for KNN with K=6 (as that is what was specified in knn_spec)
• It is the average accuracy obtained from the 5 validation sets

• filter(.metric == "accuracy") to ignore the other metric
• The collect_metrics function is used to aggregate the mean and standard error of the classifier’s validation accuracy across the folds.
• see collect_metrics(knn_cv_fit, summarize = FALSE) for the individual values

Deeper look into CV metrics

id	.metric	.estimate
Fold1	accuracy	0.8488372
Fold2	accuracy	0.8255814
Fold3	accuracy	0.8235294
Fold4	accuracy	0.8235294
Fold5	accuracy	0.8333333

\[\begin{equation} \dfrac{0.849 + 0.826 + 0.824 + 0.824 + 0.833 }{5} = 0.831 \end{equation}\]

Comments

• The standard error (std_err) is a measure of how uncertain we are in the mean value.

• Roughly speaking, we can expect the true average accuracy of the classifier to be somewhere roughly between 83% and 83% (mean \(\pm\) std_err)

• You may ignore the other columns in the metrics data frame, as they do not provide any additional insight.

• You can also ignore the entire second row with roc_auc as this metric is beyond the scope of this course.

More folds

cancer_vfold <- vfold_cv(cancer_train, v = 10, strata = Class)

vfold_metrics <- knn_wflow |>
                  fit_resamples(resamples = cancer_vfold) |>
                  collect_metrics()

vfold_metrics

# A tibble: 2 × 6
  .metric  .estimator  mean     n std_err .config             
  <chr>    <chr>      <dbl> <int>   <dbl> <chr>               
1 accuracy binary     0.847    10 0.0131  Preprocessor1_Model1
2 roc_auc  binary     0.918    10 0.00686 Preprocessor1_Model1

In practice, 5- or 10-fold are popular choices

don’t want to go too small or too big

Parameter value selection

We now want to do these for a range of possible values of K. If we go back to our original model specification, we can make the following tweaks:

knn_spec <- nearest_neighbor(weight_func = "rectangular",
                             neighbors = tune()) |> # instead of 6
  set_engine("kknn") |>
  set_mode("classification")

The tidymodels package collection provides a very simple syntax for tuning models: each parameter in the model to be tuned should be specified as tune() in the model specification rather than given a particular value

Possible values

While we could conceivable, do all possible values from 1 to \(n\) (the number of observations in our training set), we will see that the optimal choice for K will come much earlier than \(n\) = 426.

k_vals <- tibble(neighbors = seq(from = 1, to = 100, by = 5))

Then instead of using fit or fit_resamples, we will use the tune_grid function to fit the model for each value in a range of parameter values.

can’t use the workflow from before since it has the old specs

Perform CV on the grid

knn_results <- workflow() |>
  add_recipe(cancer_recipe) |>
  add_model(knn_spec) |>
  tune_grid(resamples = cancer_vfold, grid = k_vals) |>
  collect_metrics() 
knn_results

# A tibble: 40 × 7
   neighbors .metric  .estimator  mean     n std_err .config              
       <dbl> <chr>    <chr>      <dbl> <int>   <dbl> <chr>                
 1         1 accuracy binary     0.822    10 0.0133  Preprocessor1_Model01
 2         1 roc_auc  binary     0.812    10 0.0150  Preprocessor1_Model01
 3         6 accuracy binary     0.847    10 0.0131  Preprocessor1_Model02
 4         6 roc_auc  binary     0.918    10 0.00686 Preprocessor1_Model02
 5        11 accuracy binary     0.857    10 0.0129  Preprocessor1_Model03
 6        11 roc_auc  binary     0.928    10 0.00895 Preprocessor1_Model03
 7        16 accuracy binary     0.857    10 0.0183  Preprocessor1_Model04
 8        16 roc_auc  binary     0.929    10 0.00898 Preprocessor1_Model04
 9        21 accuracy binary     0.866    10 0.0149  Preprocessor1_Model05
10        21 roc_auc  binary     0.929    10 0.00917 Preprocessor1_Model05
# ℹ 30 more rows

tune_grid tunes the hyperparameters of the KNN model. It uses cross-validation with resamples specified by cancer_vfold and it tests the model with different values of the hyperparameter k, specified in the k_vals grid. This helps find the best k for the KNN model.

Accuracy check

accuracies <- knn_results |>
  filter(.metric == "accuracy")

accuracies

# A tibble: 20 × 7
   neighbors .metric  .estimator  mean     n std_err .config              
       <dbl> <chr>    <chr>      <dbl> <int>   <dbl> <chr>                
 1         1 accuracy binary     0.822    10  0.0133 Preprocessor1_Model01
 2         6 accuracy binary     0.847    10  0.0131 Preprocessor1_Model02
 3        11 accuracy binary     0.857    10  0.0129 Preprocessor1_Model03
 4        16 accuracy binary     0.857    10  0.0183 Preprocessor1_Model04
 5        21 accuracy binary     0.866    10  0.0149 Preprocessor1_Model05
 6        26 accuracy binary     0.859    10  0.0136 Preprocessor1_Model06
 7        31 accuracy binary     0.843    10  0.0152 Preprocessor1_Model07
 8        36 accuracy binary     0.848    10  0.0149 Preprocessor1_Model08
 9        41 accuracy binary     0.846    10  0.0171 Preprocessor1_Model09
10        46 accuracy binary     0.855    10  0.0160 Preprocessor1_Model10
11        51 accuracy binary     0.850    10  0.0157 Preprocessor1_Model11
12        56 accuracy binary     0.846    10  0.0185 Preprocessor1_Model12
13        61 accuracy binary     0.853    10  0.0136 Preprocessor1_Model13
14        66 accuracy binary     0.853    10  0.0140 Preprocessor1_Model14
15        71 accuracy binary     0.855    10  0.0147 Preprocessor1_Model15
16        76 accuracy binary     0.855    10  0.0147 Preprocessor1_Model16
17        81 accuracy binary     0.846    10  0.0178 Preprocessor1_Model17
18        86 accuracy binary     0.846    10  0.0197 Preprocessor1_Model18
19        91 accuracy binary     0.853    10  0.0174 Preprocessor1_Model19
20        96 accuracy binary     0.852    10  0.0131 Preprocessor1_Model20

Plotting accuracy

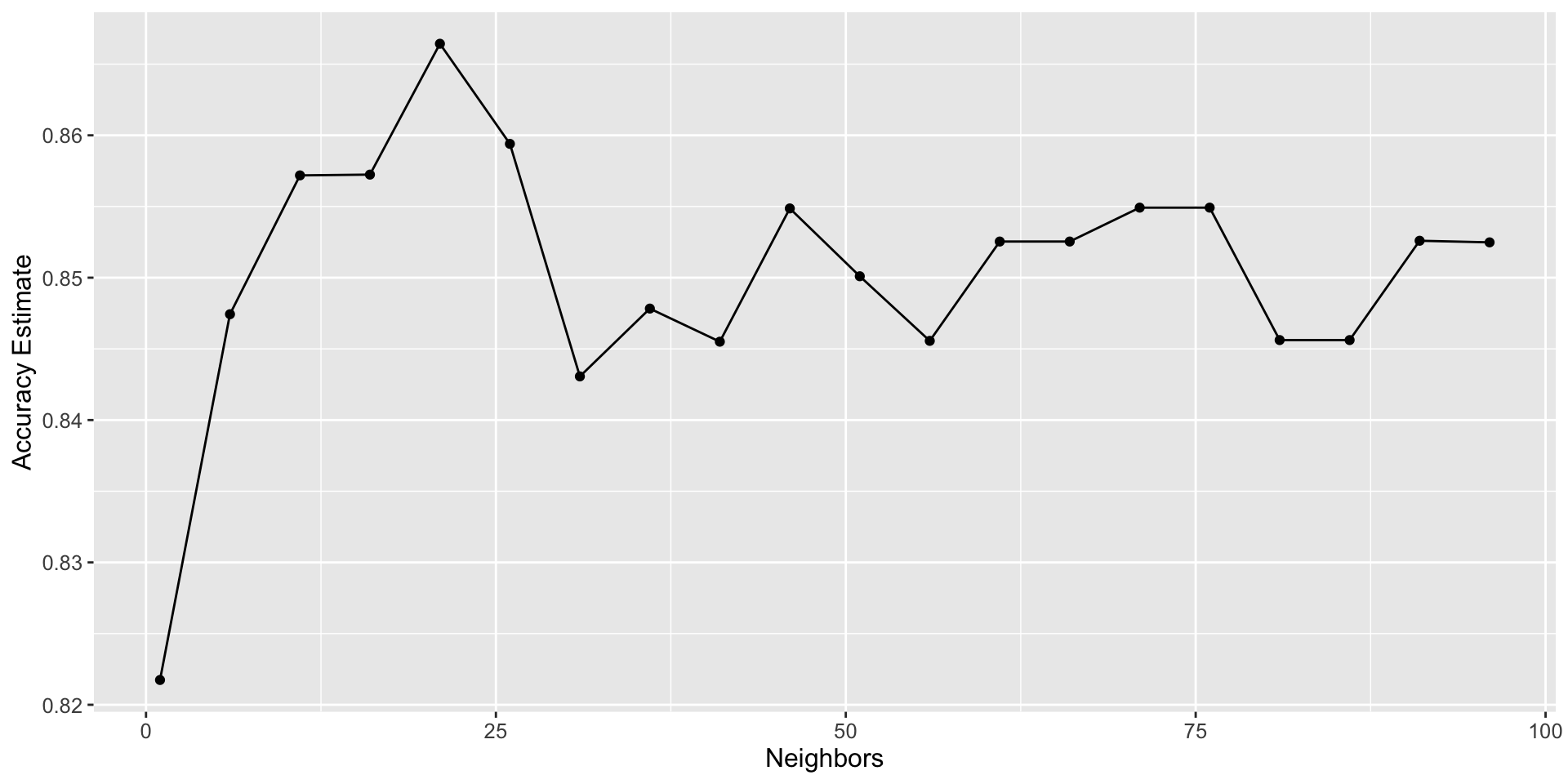
We can decide which number of neighbors is best by plotting the accuracy versus K

accuracy_vs_k <- ggplot(accuracies, aes(x = neighbors, y = mean)) +
  geom_point() +
  geom_line() +
  labs(x = "Neighbors", y = "Accuracy Estimate") + 
  theme(text = element_text(size = 12))

accuracy_vs_k

Plotting accuracy

Best K?

ind = which.max(accuracies$mean)
bestK = accuracies$neighbors[ind]
high_acc = max(accuracies$mean)

• Setting the number of nearest neighbours to K = bestK provides the highest accuracy (87%)
• But there is no exact or perfect answer here; K= and K= would be reasonably justified, as all of these differ in classifier accuracy by a small amount.
• Remember: the values you see on this plot are estimates of the true accuracy of our classifier.
• Although K = bestK value is higher than the others on this plot, that doesn’t mean the classifier is actually more accurate with this parameter value!

• prediction regions using different values of k
• the 20 k looks the most reasonable from this four choices (which is consistent with what we found using CV)
• underfitting vs. overfitting

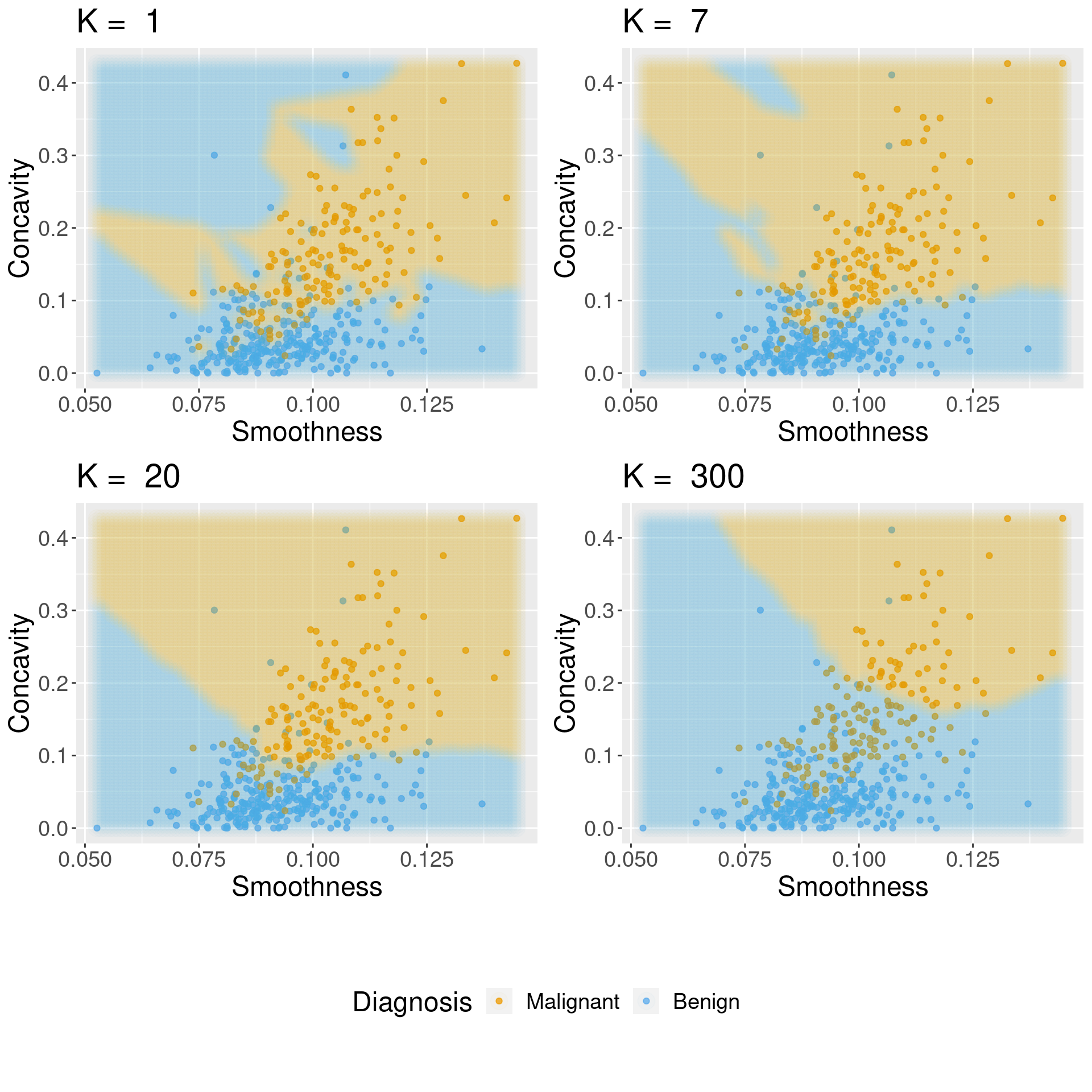
Comment

Generally, when selecting K (and other parameters for other predictive models), we are looking for a value where:

• we get roughly optimal accuracy, so that our model will likely be accurate;
• changing the value to a nearby one (e.g., adding or subtracting a small number) doesn’t decrease accuracy too much, so that our choice is reliable in the presence of uncertainty;
• the cost of training the model is not prohibitive (e.g., in our situation, if K is too large, predicting becomes expensive!).

We know that K=�= 41 provides the highest estimated accuracy. Further, Figure 6.5 shows that the estimated accuracy changes by only a small amount if we increase or decrease K� near K=�= 41. And finally, K=�= 41 does not create a prohibitively expensive computational cost of training. Considering these three points, we would indeed select K=�= 41 for the classifier.

Summary