Lecture 7: Data Visualization

DATA 101: Making Prediction with Data

Dr. Irene Vrbik

University of British Columbia Okanagan

Background

• One of the most important aspects of data analysis is the generation of proper graphics.
• One of the main reasons data analysts turn to R is for its strong graphic capabilities.
• R’s model for constructing plots strikes a balance between structure and flexibility.
• The lecture will introduce some of the basic plotting features of R and explore some controls over their graphical components.

Basic Plots

Basic Plots

• The first few slides will discuss some popular ways of displaying information graphically.
• These include:
  • Strip charts
  • Scatter plots
  • Histograms
  • Boxplots

Strip charts

• Strip charts plot the given data in order along a horizontal line.
• To create a strip chart in R, we use stripchart().
• We can think of strip charts as one-dimensional scatter plots (or dot plots).
• Naturally, strip charts are intended for one-dimensional data, that is, each observation is a single scalar value.

Strip chart

For example, let’s generate 100 observations from 1 to 10 and plot them in a strip chart.

x <- runif(n = 100, min = 1, max = 10)
stripchart(x)

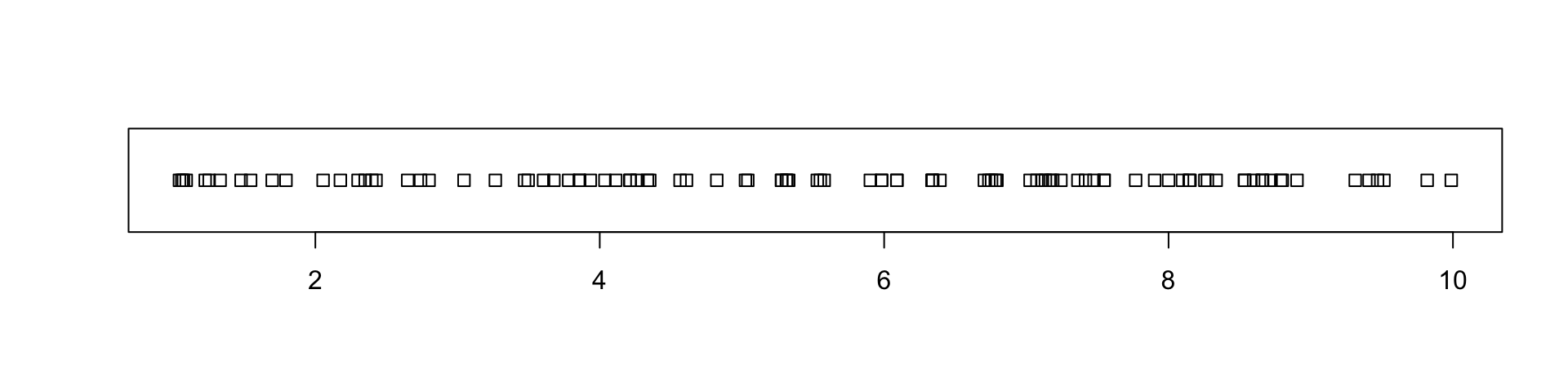
Coincident points

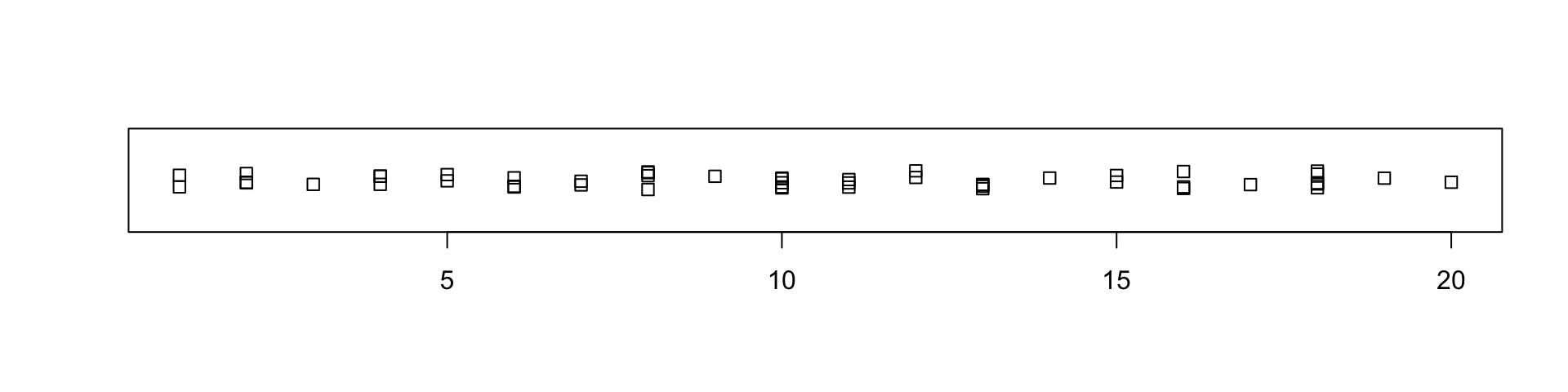
Problem what happens if we have two points with the exact same value?

You can imagine a scenario where this type of plot might be problematic.

• These “coincidence points” can be dealt with in stripchart() using the method arugment.
• The default method is to "overplot" which simply plots points on-top of each other; see ?stripchart
• Other methods include "jitter" and "stack"

Example with coicindent points

set.seed(1697037422)
x = sample(20, 50, replace=TRUE) # most numbers will be repeated

# first row = unique values
# second row = freq of value

table(x)

x
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 
 2  3  1  3  2  3  2  4  1  5  3  2  5  1  2  3  1  5  1  1 

overplot

stripchart(x)

The default method “overplot” causes such points to be overplotted, and you can’t tell how many observations fall at each value

jitter

stripchart(x, method="jitter")

but it is also possible to specify “jitter” to jitter the points,

Strip charts

stripchart(x, method="stack"); table(x)

x
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 
 2  3  1  3  2  3  2  4  1  5  3  2  5  1  2  3  1  5  1  1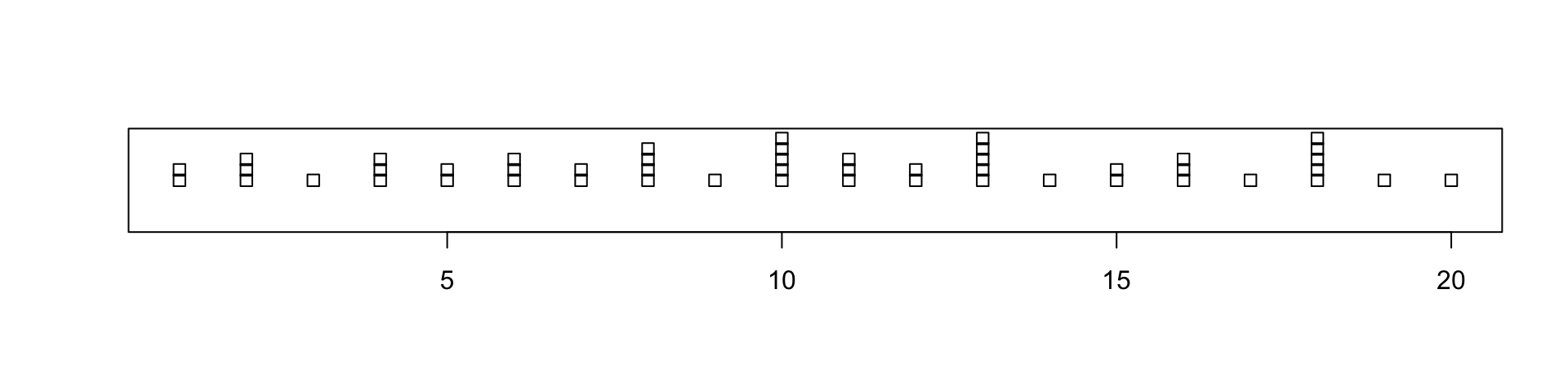 

stacked makes sense for very granular data.

Scatterplots

• If we extend the concept of the one dimensional strip charts to two dimensions, we get a scatter plot.
• Like strip charts, every observation will be represented by a single point on the chart, only now, that location will depend on two values.
• The first value gives its placement in the horizontal direction (ie. the \(x\)-axis), while the second number gives its placement in vertical direction (i.e. along the \(y\)-axis).
• Plots of this type are produced using plot() in R.

Scatterplots

x = runif(n=100)
y = runif(n=100, min=0, max=5)
plot(x,y)

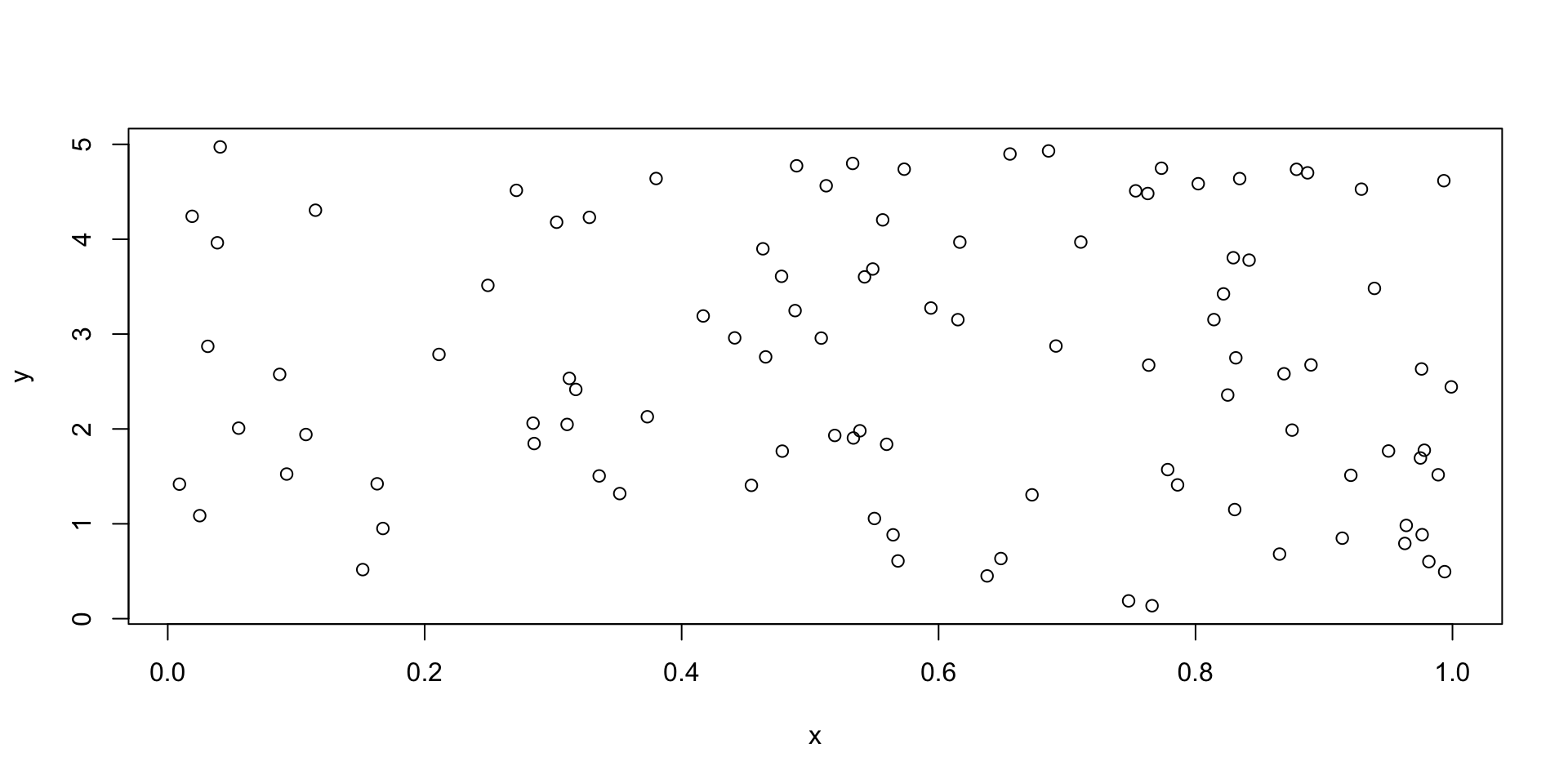
Histograms

• A histogram is very common visualization that plots the number of observations appearing within certain ranges called bins.
• Bins (or buckets) are constructed by dividing the entire range of values into a series of intervals and counting how many values fall into each interval.
• In R histograms are produced using the hist() function which tries to calculate reasonable bins automatically; however, we can manually set them ourselves in the breaks argument

%frequencies that data appears within certain ranges.

default hist

set.seed(4444); x = runif(n=100, min=1, max =10); hist(x)

adjusting breaks

hist(x, breaks = 40)

https://www.statmethods.net/graphs/density.html

Density Plots

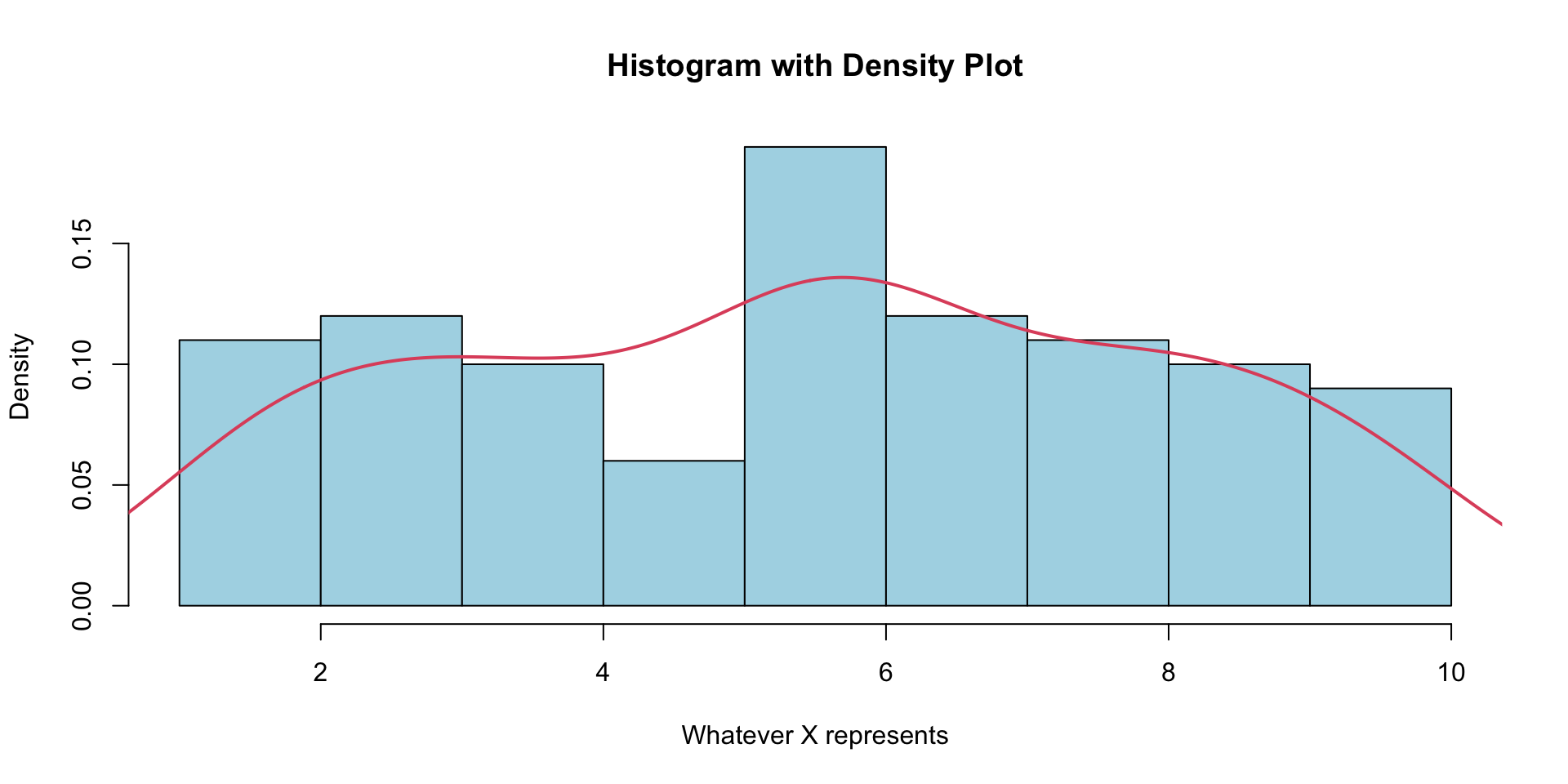
• One of the main uses of histograms is to provide a visualization of the distribution of our data.
• As exhibited in the previous example, this visualization technique can be greatly affected by the number of bins.
• We may prefer to create a smoother density plot to get a more accurate view the distribution of a variable.
• The general syntax for producing density plots is plot(density(x)).

% are usually a much more effective way to view the distribution of a variable.

density plot

plot(density(x))

compare with hist

# Create a histogram
hist(x, probability = TRUE, # to get prob instead of freq
     col = "lightblue", 
     main = "Histogram with Density Plot",
     xlab = "Whatever X represents")

# Create a density plot and overlay it
lines(density(x), 
      col = 2, # 2 = red 
      lwd = 2 # line width
      )

compare with hist

R Colours

• Notice that by setting col =2 the boxplot turned red.
• Integer col values index the colours in R’s palette().
• R’s default colour palette looks like this:

 barplot(rep(1,8), yaxt="n", col=1:8); palette()

[1] "black"   "#DF536B" "#61D04F" "#2297E6" "#28E2E5" "#CD0BBC" "#F5C710"
[8] "gray62" 

R Colours

• In words, 1 = "black", 2 = "red", and so on.
• Of course we can always call the full character name instead.
• See for example here for a gallery of colour names
• Alternatively we can redefine our colour palette so that 1="yellow", and 2="green" for example:

palette(c("yellow", "green"))

Alternative palettes can be found R packages like RColorBrewer

Graphing Parameters

• While many of the plotting features like title and axes labels can be called directly within the plotting function, it is possible to call them afterwards.
• Just like lines() superimposed a line overtop our histogram, we can superimpose text in the form of titles and labels (among other things) to a plot that has already been graphed.
• For example, we could add titles and labels for out boxplot on car mileage using the title() command.

same plot

• To see both the histogram and density curve on one plot, we use the lines() function to superimpose the density curve on top of the histogram.
• Here we use probability = TRUE (same as prob = TRUE,freq = FALSE)
• If prob = TRUE / freq = FALSE the proportion (rather frequencies) are plotted on the \(y\)-axis.

In addition to lines() we have others like it, eg. points(), abline(),. N.B. these will only work if a plot has already been called

Boxplots

• A boxplot (AKA box-and-whisker plot) provides a graphical view of the median, quartiles, maximum, and minimum of a data set.
• When applicable, it can tell identify outliers and their values.
• The plots are great when comparing groups; however, they can be misleading when there are very few data points (in which case we should probably use a strip chart).
• These plots are available through the boxplot() command.

It can also tell you if your data is symmetrical, how tightly your data is grouped, and if and how your data is skewed.

Boxplot

Image source

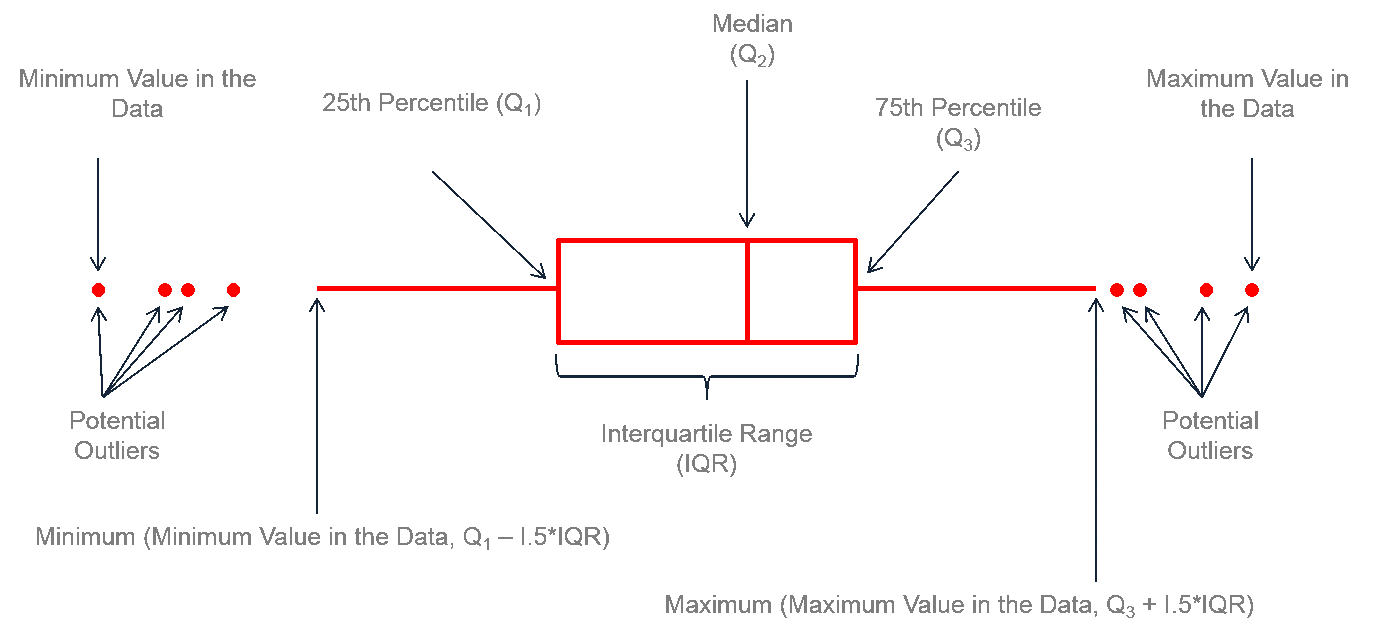
Box

• The central part of the boxplot is the “box” itself.

• It represents the interquartile range (IQR), which spans the middle 50% of the data.

• The bottom and top edges of the box correspond to the first quartile (Q1) and the third quartile (Q3), respectively.

• The height¹ of the box is determined by the range between Q1 and Q3. The box typically contains a horizontal line inside it, representing the median (Q2) of the dataset.

1. or width if you are plotting the boxplot horizontally

Quantiles vs Quartiles

Quantiles are a way to divide a dataset into equal portions¹. For boxplots we need:

• Median (Q2 or the 50th Percentile): the middle data point when dataset it is ordered from smallest to largest. It divides the data into two equal halves, with 50% of the data falling below it and 50% above it.

• First Quartile (Q1 or the 25th Percentile): Q1 divides the lowest 25% of the data from the rest. It is the data point at the 25th percentile, meaning that 25% of the data falls below it.

• Third Quartile (Q3 or the 75th Percentile): Q3 divides the lowest 75% of the data from the rest. It is the data point at the 75th percentile, meaning that 75% of the data falls below it.

common mistake that the middle line represents the mean

1. Quartiles (four parts), Quintiles (five parts), Percentiles (100 parts), Deciles (10 parts)

IQR

• The Interquartile Range (IQR) is a statistical measure that represents the range between the first quartile (Q1) and the third quartile (Q3) in a dataset.

\[IQR = Q3 - Q1\]

• IQR It is a measure of statistical dispersion and provides valuable information about the spread of data within the middle 50% of the dataset.

IQR It is a measure of statistical dispersion and provides valuable information about the spread of data within the middle 50% of the dataset.

Whiskers

• The “whiskers” extend from the box to the minimum and maximum values within a specified range.
• Commonly, the whiskers extend to the lowest data point within 1.5 times the IQR below Q1 and the highest data point within 1.5 times the IQR above Q3.
• Data points beyond these limits are often considered potential outliers and are plotted individually as dots or asterisks.

Outliers

• Outliers are individual data points that fall outside the whisker limits.
• These points are often plotted separately to draw attention to their exceptional values.
• They can be legitimate data points that indicate extreme values or errors in the data collection process.

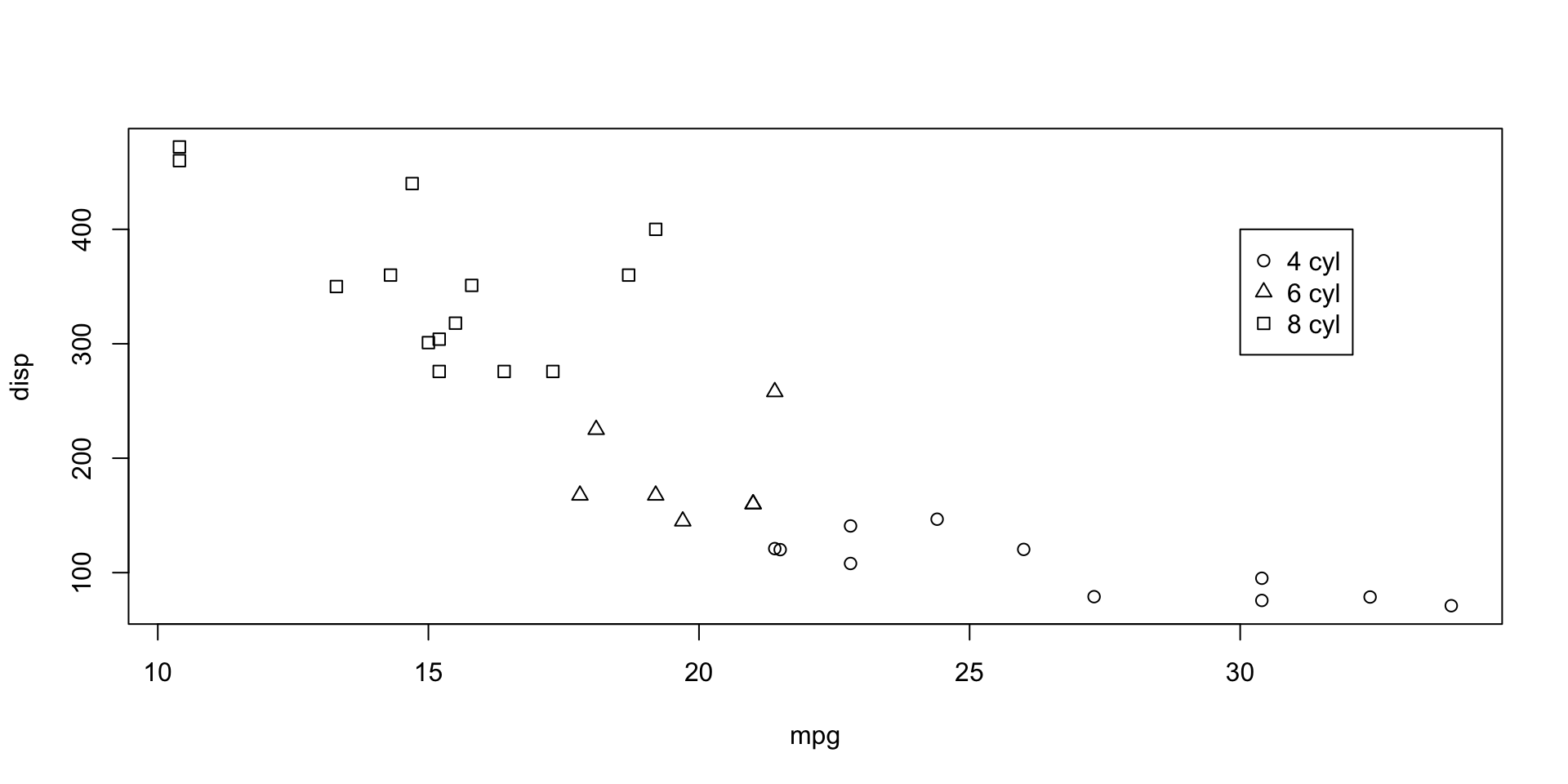
Example: mtcars

• For demonstration purposes, let’s have a look at the mtcars dataset; see ?mtcars.

• We’ll focus on

  • mpg Miles/(US) gallon
  • cyl Number of cylinders

The data was extracted from the 1974 Motor Trend US magazine and comprises the fuel consumption and 10 aspects of automobile design and performance for 32 automobiles (1973–74 models).

mtcars

boxplot(mpg~cyl,data=mtcars, main="Car Milage Data", 
        xlab="Number of Cylinders", ylab="Miles Per Gallon")

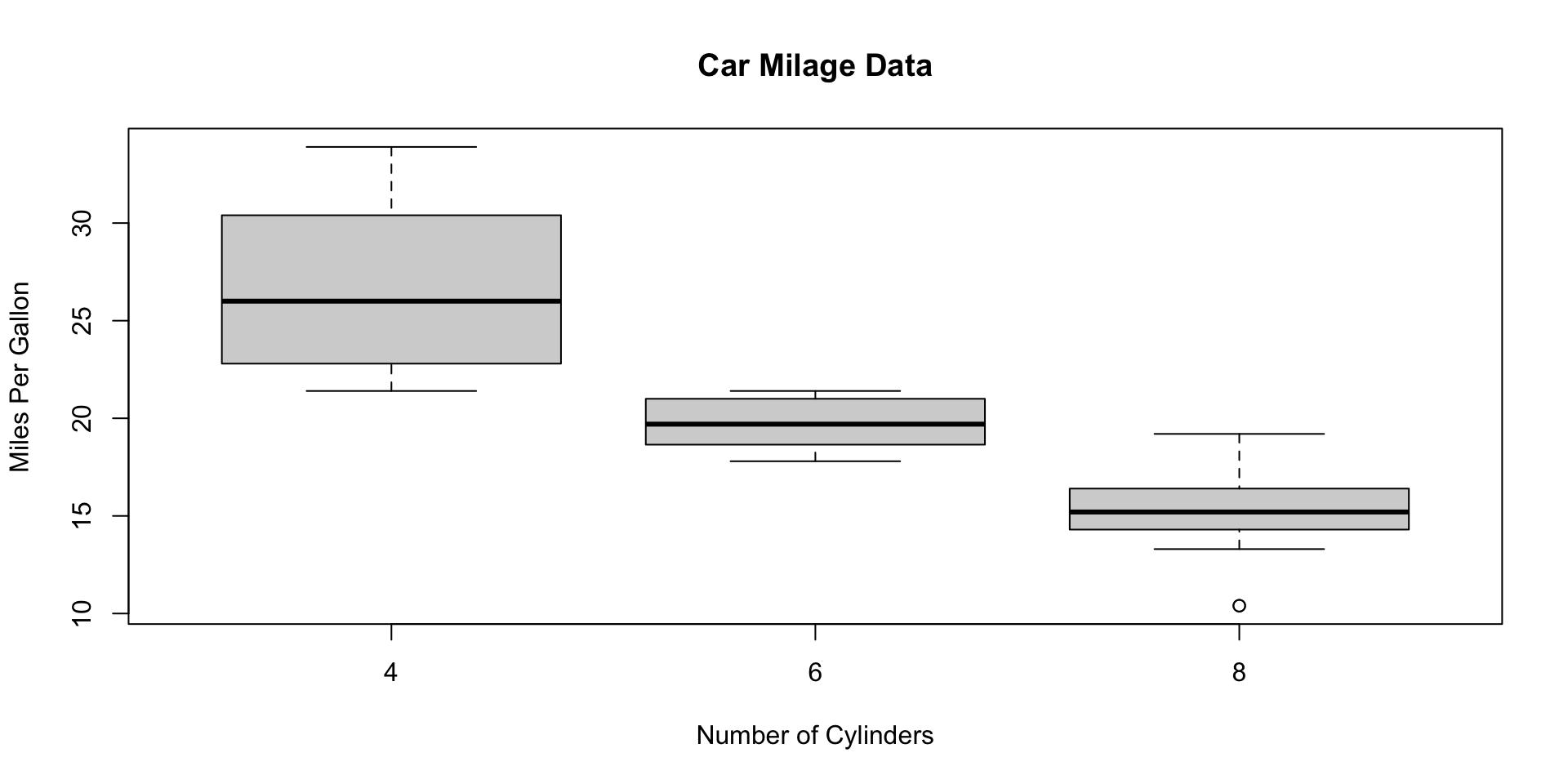
Comment

• The boxplot on this slide is a so-called side-by-side boxplot.
• We can think of it 3 boxplots in one plot.
• Starting from the left, we see a boxplot for the mpg variable for cars with 4, 6, and 8 cylinders, respectively.
• If we want to investigate the individual statistics for cars with 8 cylinders, say, we could also use subset() or split()

Boxplot with subset

cyl8 = subset(mtcars, cyl==8);boxplot(cyl8$mpg)

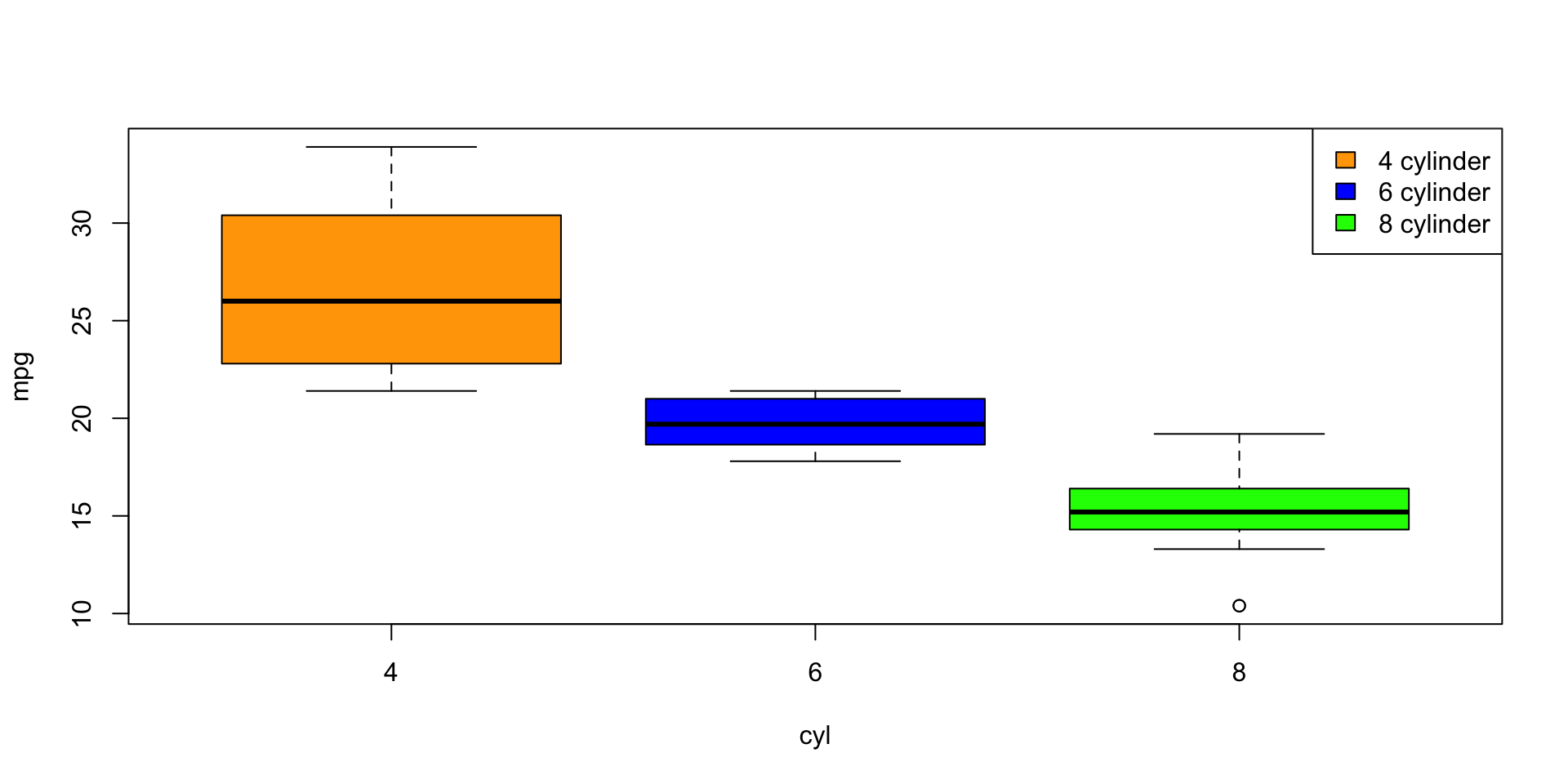
Legends

• Another useful plotting features is legends. General syntax:

legend(location, legend, ...)

• location can be specific co-ordinates or a keyword: “bottom”, “bottomleft”, “left”, “topleft”, “top”, “topright”, “right”, “bottomright”, or “center”
• legend is a vector of characters to appear in the legend.
• ... provide the characteristics, eg. col(colour), lty (line type), pch (plotting character) distinguishing the members in your legend.

boxplot(mpg~cyl,data=mtcars,  col=c("orange", "blue", "green"))
legend("topright", legend=c("4 cylinder", "6 cylinder", "8 cylinder"),
       fill = c("orange", "blue", "green"))

Plot size

• In RStudio, we can resize the image by pressing the   button¹ and use click and drag on the plotting window.
• In Rmd, the default width and height for R plots are set to 7; we can change these defaults using the fig.width and fig.height code chunk options²

We can change those dimensions using the {} and {} arguments in {}. - Using the aforementioned function also allows us plot multiple graphs at a time.

1. alternatively, we can open a new graphics window using windows(), quartz()}, or X11() on a Windows/Mac/Unix, resp.

2. out.width controls how wide you want the rendered figure. e.g. if set to “50%” the outputted plot will take up 50% of the available horizontal space in the document.

Graphing Parameters

• There are a number of graphical parameters that are available through the par() function.
• It is important to mention, that par() sets the global state for any graphical related commands.
• To put another way, all future plots in your plotting device will inherit this change (that is, until you open a new session, close the plotting device via dev.off() or change them back to their default).
• To see the complete set of graphical parameters, type ?par

Graphing Parameters

There are 2 margin areas in R:

• mar() for margin
• oma() for outer margin

You can specify the desired space in the bottom, left, top and right using the syntax:

par(mar= c(b, l, t, r))

[Image source]

The units are in lines (see image)

par defaults

To see the default setting (assuming you have redefined them already):

par()$mar

[1] 5.1 4.1 4.1 2.1

par()$oma

[1] 0 0 0 0

It is useful to sometimes change the defaults to remove excessive white space

# Margins area
par(oma=c(3,3,3,3))  # all sides have 3 lines of space  
par(mar=c(5,4,4,2) + 0.1)   # default margins

Exercise 1

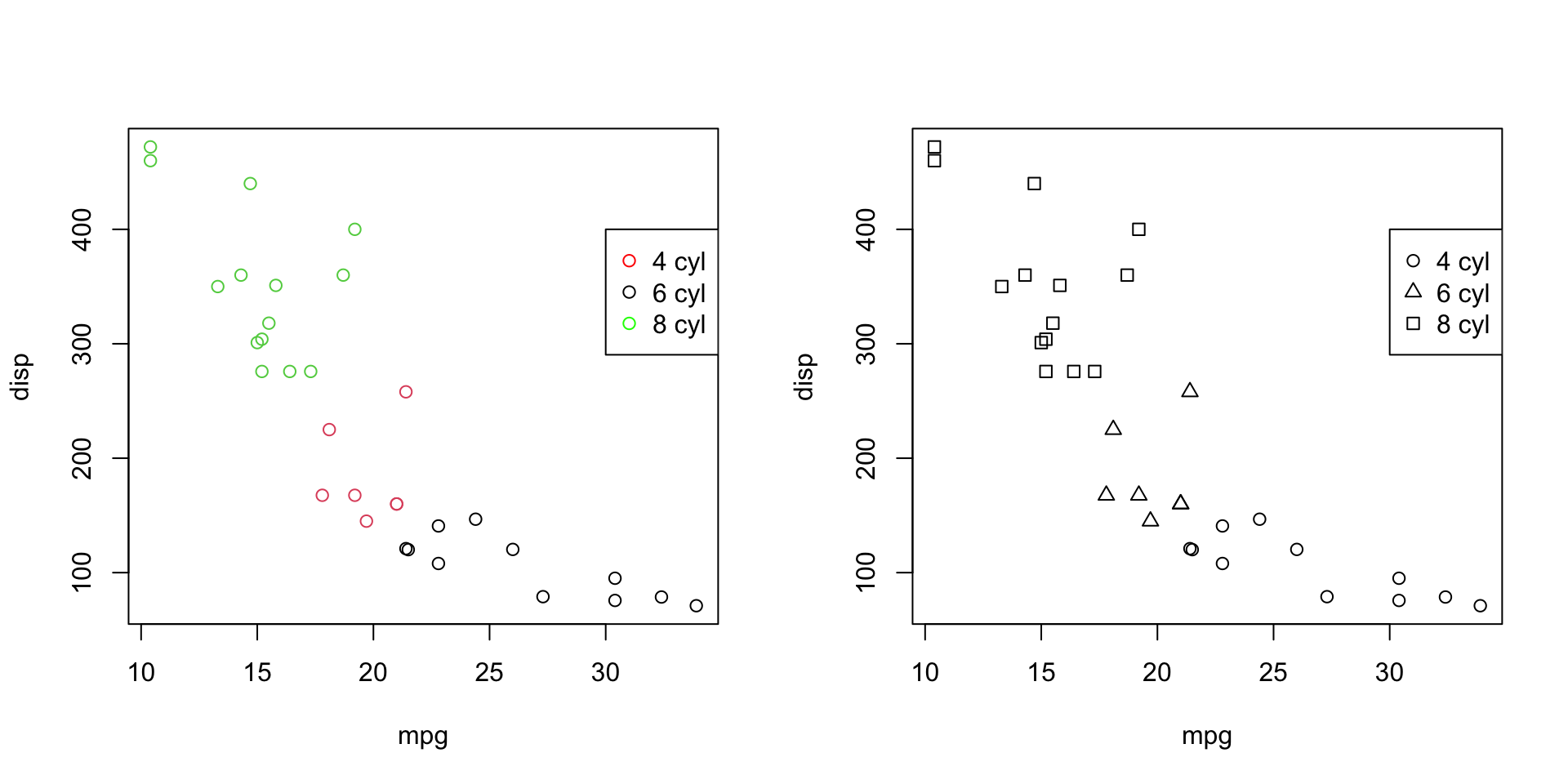
Create a legend that labels points by the number of cylinders cyl. Use red, black, and green for the values or 4, 6, and 8, respectively.

Code

attach(mtcars)
plot(mpg, disp, col=factor(cyl, labels = c("red", "black", "green")))
legend(30, 400, legend=c("4 cyl", "6 cyl", "8 cyl"), pch = 1, col=c("red", "black", "green"))

Exercise 1

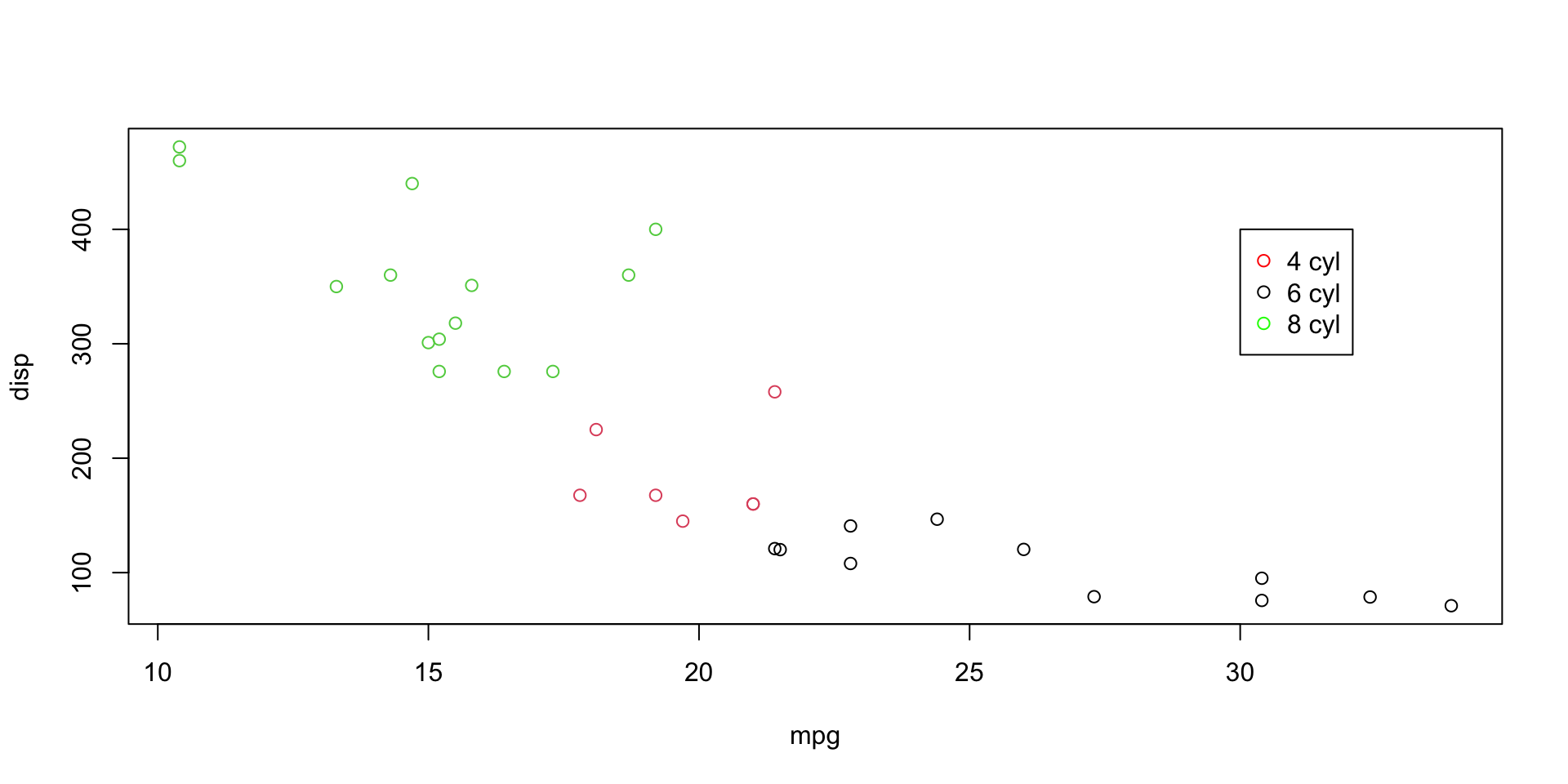
Exercise 2

Create a scatterplot for mpg vs. disp. Create a legend that labels points by the number of cylinders cyl. Use circles, triangles, and squares for the values or 4, 6, and 8, respectively.

Code

pchvec <- replace(cyl,cyl==4, 1)
pchvec <- replace(pchvec, pchvec==6, 2)
pchvec <- replace(pchvec, pchvec==8, 0)

plot(mpg, disp, pch=pchvec)
legend(30, 400, legend=c("4 cyl", "6 cyl", "8 cyl"), pch = c(1,2,0))

Exercise 2

par mar

• Another helpful graphical parameter setting (recall other on this slide) is mfrow, mfcol

• This expects a vector of the form c(nr, nc).

• Subsequent figures will be drawn in an nr-by-nc array on the device by columns (mfcol), or rows (mfrow), respectively.

par(mfrow=c(1, 2)) # 1 row, 2 columns
plot(mpg, disp, col=factor(cyl, labels = c("red", "black", "green")))
legend(30, 400, legend=c("4 cyl", "6 cyl", "8 cyl"), pch = 1, col=c("red", "black", "green"))
plot(mpg, disp, pch=pchvec)
legend(30, 400, legend=c("4 cyl", "6 cyl", "8 cyl"), pch = c(1,2,0))

par mar

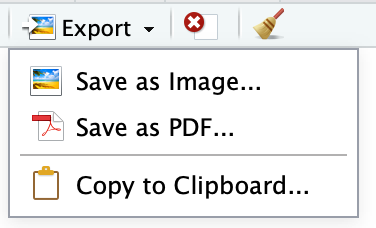
Saving plots

You can save the graph using a variety of methods in R:

1. In (base) R: File > Save As
2. Using the Export button in RStudio:

3. Through R commands like: pdf(), png(), jpeg(), svg(), depending on the file format you want to use.

Example

Once you’ve completed your plotting with, you can then use one of these file output functions to save the plot to a file depending on the formation you want. Here’s an example using the pdf() function to save a plot to a PDF file:

# Open a PDF file for plotting
pdf("boxplot.pdf", width=10, height = 5) # saves to working directory

# Plot will be sent to the PDF file
boxplot(mpg~cyl,data=mtcars, main="Car Milage Data")

# Close the PDF device
dev.off()

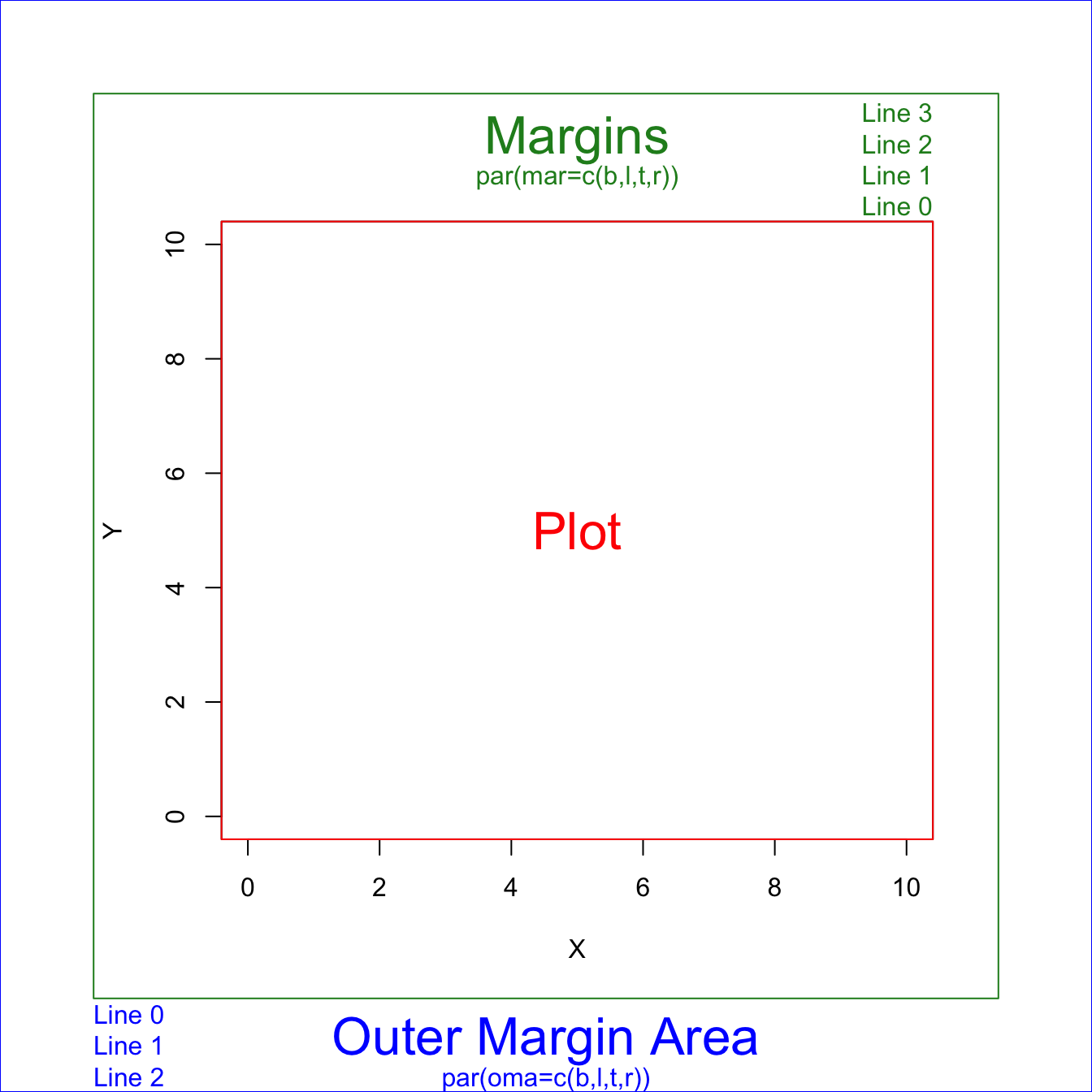
Comments

• Before we make our plot we first open a PDF file using pdf("boxplot.pdf"), and any subsequent plots will be directed to this PDF file.

• After completing the plot, we close the PDF device using dev.off().

• You can replace "boxplot.pdf" with the file path and name you want to use; otherwise it will get saved to your working directory.

• The same approach applies to other file formats; you can use png(), jpeg(), svg(), or tiff() instead of pdf() to save plots in those formats.