Lab Tutorial 6

Summary: The content of this tutorial has been shamelessly obtained from the textbook worksheet on Classification II: Evaluation & Tuning,ensuring a comprehensive understanding of model performance metrics and evaluation techniques.

Towards the end of the lab, you will find a set of assignment exercises (Assignment 5). These assignments are to be completed and submitted on Canvas.

Lab 06

After completing this week’s lecture and tutorial work, you will be able to:

• Describe what a test data set is and how it is used in classification.

• Using R, evaluate classification accuracy using a test data set and appropriate metrics.

• Using R, execute cross-validation in R to choose the number of neighbours.

• In a dataset with > 2 attributes/features, perform k-nearest neighbour classification in R using the tidymodels package to predict the class of a test dataset.

• Describe advantages and disadvantages of the k-nearest neighbour classification algorithm.

### Run this cell before continuing. 
library(tidyverse)
library(repr)
library(tidymodels)
options(repr.matrix.max.rows = 6)

Randomness and Setting Seeds

This tutorial uses functions from the tidymodels library, which not only allows us to perform K-nearest neighbour classification, but also allows us to evaluate how well our classification worked. In order to ensure that the steps in the worksheet are reproducible, we need to set a seed, i.e., a numerical “starting value,” which determines the sequence of random numbers R will generate.

Below in many cells we have included a call to set.seed. Do not remove these lines of code; they are necessary to make sure the autotesting code functions properly.

The reason we have set.seed in so many places is that our file is organized into cells that can be run out of order. Since things can be run out of order, the exact sequence of random values that is used in each cell is hard to determine, which makes autotesting really difficult. One drawback of calling set.seed everywhere is that the numbers that will be generated won’t really be random. For the purposes of teaching and learning, that is fine here. But in other data analyses outside of this course, you must call set.seed only once at the beginning of the analysis, so that your random numbers are actually reasonably random.

Fruit Data Example - (Part II)

You will recognize a few of the first questions from last week’s tutorial. This will help you repeat some of the fundamentals of classification before tackling the later questions in this tutorial, which integrate concepts you learned from this week’s material. First, load the file fruit_data.csvfrom the previous tutorial into your notebook.

mutate() the fruit_name column such that it is a factor using as_factor().

Assign your data to an object called fruit_data.

Click for answer

fruit_data <- read_csv("../data/fruit_data.csv") |>
              mutate(fruit_name = as.factor(fruit_name))

Rows: 59 Columns: 7
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (2): fruit_name, fruit_subtype
dbl (5): fruit_label, mass, width, height, color_score

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

Using mass and width, calculate the distance between the first observation and the 44th observation. Assign your answer to an object called fruit_dist_44.

Click for answer

fruit_dist_44 <- fruit_data |>
  slice(1,44)|>
  select(mass, width)|>
  dist()

Create a tidymodels recipe to standardize (i.e., center and scale) all of the variables in the fruit dataset. Specify your recipe with class variable fruit_name and predictors mass, width andheight. Name the recipe fruit_data_recipe. Use set.seed(9999).

Click for answer

set.seed(9999) 

fruit_data_recipe <- recipe(fruit_name ~ mass+width+height, data = fruit_data) |> step_center(all_predictors()) |>
 step_scale(all_predictors()) |>
  prep()

Use bake to apply recipe to your original data. Save the scaled data to scaled_fruit_data.

Click for answer

scaled_fruit_data <- bake(fruit_data_recipe, fruit_data)

Evaluating the Model

To add evaluation into our classification pipeline, we:

1. Split our data into two subsets: training data and testing data.
2. Build the model & choose K using training data only (sometimes called tuning)
3. Compute accuracy by predicting labels on testing data only.

We’ll now talk about each step individually.

1. Split our data into two subsets (a training and test set)

In this part, we will be partitioning fruit_data into a training (75%) and testing (25%) set using the tidymodels package. After creating the test set, we will put the test set away in a lock box and not touch it again until we have found the best k-nn classifier we can make using the training set. We will use the variable fruit_name as our class label.

To create the training and test set, first use the initial_split function to split fruit_data. Specify you want to use 75% of the data. For the strata argument, place the variable we want to classify, fruit_name. Name the object you create fruit_split.

Next, pass the fruit_split object to the training and testing functions and name your respective objects fruit_train and fruit_test.

# Set the seed. Don't remove this!
set.seed(3456) 

# Randomly take 75% of the data in the training set. 
# This will be proportional to the different number of fruit names in the dataset.

#... <- initial_split(..., prop = ..., strata = ...)  
#... <- training(...)   
#... <- testing(...)

Click for answer

set.seed(3456) 

fruit_split <- initial_split(fruit_data, prop = 0.75, strata = fruit_name)  
fruit_train <- training(fruit_split)   
fruit_test <- testing(fruit_split)

So far, we have split the training and testing datasets as well as preprocessed the data. Now, let’s create our K-nearest neighbour classifier with only the training set using the tidymodels package. First, create the classifier by specifying that we want \(K = 3\) neighbors and that we want to use the straight-line distance which is the same as Euclidean distance. Assign your answer to an object called knn_spec.

Next, train the classifier with the training data set using the workflow function. This function allows you to bundle together your pre-processing, modeling, and post-processing requests. Scaffolding is provided below for you. Assign your answer to an object called fruit_fit.

set.seed(2020) # DO NOT REMOVE

#... <- nearest_neighbor(weight_func = ..., neighbors = ...) |>
#       set_engine(...) |>
#       set_mode(...)

#... <- workflow() |>
#       add_recipe(...) |>
#       add_model(...) |>
#       fit(data = ...)

Click for answer

set.seed(2020) # DO NOT REMOVE

knn_spec <- nearest_neighbor(weight_func = "rectangular", neighbors = 3) |>
      set_engine("kknn") |>
       set_mode("classification")

fruit_fit <- workflow() |>
  add_recipe(fruit_data_recipe) |>
  add_model(knn_spec) |>
  fit(data = fruit_train)

fruit_fit

══ Workflow [trained] ══════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: nearest_neighbor()

── Preprocessor ────────────────────────────────────────────────────────────────
2 Recipe Steps

• step_center()
• step_scale()

── Model ───────────────────────────────────────────────────────────────────────

Call:
kknn::train.kknn(formula = ..y ~ ., data = data, ks = min_rows(3,     data, 5), kernel = ~"rectangular")

Type of response variable: nominal
Minimal misclassification: 0.1627907
Best kernel: rectangular
Best k: 3

Now that we have created our K-nearest neighbor classifier object, let’s predict the class labels for our test set.

First, pass your fitted model and the test dataset to the predict function. Then, use the bind_cols function to add the column of predictions to the original test data.

Assign your answer to an object called fruit_test_predictions.

set.seed(2020) # DO NOT REMOVE

#... <- predict(... , ...) |>
#       ...(...)

Click for answer

set.seed(2020) # DO NOT REMOVE

fruit_test_predictions <- predict(fruit_fit, fruit_test) |>
  bind_cols(fruit_test)


fruit_test_predictions

# A tibble: 16 × 8
   .pred_class fruit_label fruit_name fruit_subtype     mass width height
   <fct>             <dbl> <fct>      <chr>            <dbl> <dbl>  <dbl>
 1 apple                 1 apple      granny_smith       180   8      6.8
 2 mandarin              2 mandarin   mandarin            80   5.9    4.3
 3 orange                1 apple      braeburn           178   7.1    7.8
 4 orange                1 apple      golden_delicious   164   7.3    7.7
 5 apple                 1 apple      golden_delicious   156   7.7    7.1
 6 apple                 1 apple      cripps_pink        170   7.6    7.9
 7 apple                 3 orange     selected_seconds   140   6.7    7.1
 8 apple                 3 orange     selected_seconds   164   7.2    7  
 9 orange                3 orange     turkey_navel       190   7.5    8.1
10 apple                 3 orange     turkey_navel       154   7.3    7.3
11 apple                 3 orange     turkey_navel       144   6.8    7.4
12 lemon                 4 lemon      spanish_belsan     194   7.2   10.3
13 lemon                 4 lemon      spanish_belsan     200   7.3   10.5
14 lemon                 4 lemon      spanish_belsan     186   7.2    9.2
15 lemon                 4 lemon      unknown            118   5.9    8  
16 lemon                 4 lemon      unknown            116   5.9    8.1
# ℹ 1 more variable: color_score <dbl>

Great! We have now computed some predictions for our test datasets! From glancing at the dataframe above, it looks like most of them are correct, but wouldn’t it be interesting if we could find out our classifier’s accuracy?

Thankfully, the metrics function from the tidymodels package can help us. To get the statistics about the quality of our model, you need to specify the truth and estimate arguments. In the truth argument, you should put the column name for the true values of the response variable. In the estimate argument, you should put the column name for response variable predictions.

Assign your answer to an object called fruit_prediction_accuracy.

set.seed(2020)
#... <- fruit_test_predictions |>
#         ...(truth = ..., estimate = ...)             

Click for answer

set.seed(2020)
fruit_test_predictions |>
  metrics(truth = fruit_name, estimate = .pred_class) |>
  filter(.metric == "accuracy")            

# A tibble: 1 × 3
  .metric  .estimator .estimate
  <chr>    <chr>          <dbl>
1 accuracy multiclass     0.625

Now, let’s look at the confusion matrix for the classifier. This will show us a table comparing the predicted labels with the true labels.

A confusion matrix is essentially a classification matrix. The columns of the confusion matrix represent the actual class and the rows represent the predicted class (or vice versa). Shown below is an example of a confusion matrix.

		Actual Values
		Positive	Negative
Predicted Value	Positive	True Positive	False Positive
	Negative	False Negative	True Negative

• A true positive is an outcome where the model correctly predicts the positive class.
• A true negative is an outcome where the model correctly predicts the negative class.
• A false positive is an outcome where the model incorrectly predicts the positive class.
• A false negative is an outcome where the model incorrectly predicts the negative class.

We can create a confusion matrix by using the conf_mat function. Similar to the metrics function, you will have to specify the truth and estimate arguments. Assign your answer to an object called fruit_mat.

set.seed(2020) # DO NOT REMOVE

#... <- fruit_test_predictions |> 
#       ...(truth = ..., estimate = ...)

Click for answer

set.seed(2020)
fruit_mat <- fruit_test_predictions |>
             conf_mat(truth = fruit_name, estimate = .pred_class)       
fruit_mat

          Truth
Prediction apple lemon mandarin orange
  apple        3     0        0      4
  lemon        0     5        0      0
  mandarin     0     0        1      0
  orange       2     0        0      1

Reading fruit_mat, how many observations were labelled correctly?

A. 16

B. 12

C. 10

D. 13

2. Cross-validation

The vast majority of predictive models in statistics and machine learning have parameters that you have to pick. For the past few exercises, we have had to pick the number of neighbours for the class vote, which we have done arbitraily. But, is it possible to make this selection, i.e., tune the model, in a principled way? Ideally, we want to pick the number of neighborurs to maximize the performance of our classifier on data it hasn’t seen yet.

An important aspect of the tuning process is that we can, if we want to, split our training data again, train and evaluate a classifier for each split, and then choose the parameter based on all of the different results. If we just split our training data once, our best parameter choice will depend strongly on the randomness from how this single split was made. Using multiple different splits, we’ll get a more robust estimate of accuracy, which will lead to a more suitable choice of the number of neighbours \(K\) to perform well on unseen data.

The idea of training and evaluating models on multiple training data splits times is called “cross-validation”. In cross-validation, we split our overall training data into \(C\) evenly-sized chunks, and then iteratively use 1 chunk as the validation set and combine the remaining \(C−1\) chunks as the training set. The validation set is used in a similar was as the test set, except that the test set is only used once at the end to report model performance whether we use model performance on the validation set to select the model during cross-validation.

---

We can perform a cross-validation in R using the vfold_cv function. To use this function, you have to identify the training set as well as specify the v (the number of folds) and the strata argument (the label variable). For this exercise, perform \(5\)-fold cross-validation.

Assign your answer to an object called fruit_vfold.

set.seed(2020) # DO NOT REMOVE

#... <- vfold_cv(..., v = ..., strata = ...)

Click for answer

set.seed(2020)
fruit_vfold <- vfold_cv(fruit_train, v = 5, strata = fruit_name)

Now perform the workflow analysis again. You can reuse the fruit_recipe and knn_spec objects you made earlier. When you are fitting the knn model, use the fit_resamples function instead of the fit function for training. This function will allow us to run a cross-validation on each train/validation split we created in the previous question.

Assign your answer to an object called fruit_resample_fit.

set.seed(2020) # DO NOT REMOVE

#... <- workflow() |>
#       add_recipe(...) |>
#       add_model(...) |>
#       fit_resamples(resamples = ...)

Click for answer

set.seed(2020)
fruit_resample_fit <- workflow() |>
                      add_recipe(fruit_data_recipe) |>
                      add_model(knn_spec) |>
                      fit_resamples(resamples = fruit_vfold)

→ A | warning: No observations were detected in `truth` for level(s): 'mandarin'
               Computation will proceed by ignoring those levels.

There were issues with some computations   A: x1

There were issues with some computations   A: x3

Now that we have ran a cross-validation on each train/validation split, one has to ask, how accurate was the classifier’s validation across the folds? We can aggregate the mean and standard error by using the collect_metrics function. The standard error is essentially a measure of how uncertain we are in the mean value.

Use the collect_metrics function on the fruit_resample_fit object and assign your answer to an object called fruit_metrics.

Click for answer

fruit_resample_fit |> 
  collect_metrics() 

# A tibble: 2 × 6
  .metric  .estimator  mean     n std_err .config             
  <chr>    <chr>      <dbl> <int>   <dbl> <chr>               
1 accuracy multiclass 0.763     5  0.0378 Preprocessor1_Model1
2 roc_auc  hand_till  0.933     5  0.0282 Preprocessor1_Model1

4. Parameter value selection

Using a 5-fold cross-validation, we have established a prediction accuracy for our classifier.

If we had to improve our classifier, we have to change the parameter: number of neighbours, \(K\). Since cross-validation helps us evaluate the accuracy of our classifier, we can use cross-validation to calculate an accuracy for each value of \(K\) in a reasonable range, and then pick the value of \(K\) that gives us the best accuracy.

The great thing about the tidymodels package is that it provides a very simple syntax for tuning models. Using tune(), each parameter in the model can be adjusted rather than given a specific value.

Create a new K-nearest neighbor model specification but instead of specifying a particular value for the neighbors argument, insert tune().

Assign your answer to an object called knn_tune.

#write code

Click for answer

knn_tune <- nearest_neighbor(weight_func = "rectangular", 
                             neighbors = tune()) |>
  set_engine("kknn") |>
  set_mode("classification")

Now, create a workflow() analysis that combines fruit_recipe and our new knn_tune model specification.

Instead of using fit or fit_resamples, we will use the tune_grid function to fit the model for each value in a range of parameter values. For the resamples argument, input the cross-validation fruit_vfold model we created earlier. The grid argument specifies that the tuning should try \(X\) amount of values of the number of neighbors \(K\) when tuning. For this exercise, use 10 \(K\) values when tuning which is specified by k_vals.

Finally, aggregate the mean and standard error by using the collect_metrics function.

Assign your answer to an object called knn_results.

set.seed(1234) # set the seed, don't remove this
k_vals <- tibble(neighbors = seq(from = 1, to = 10, by = 1))
#... <- workflow() |>
#       add_recipe(...) |>
#       add_model(...) |>
#       tune_grid(resamples = ..., grid = ...) |>
#       ...

Click for answer

set.seed(1234) # set the seed, don't remove this
k_vals <- tibble(neighbors = seq(from = 1, to = 10, by = 1))
knn_results <- workflow() |>
       add_recipe(fruit_data_recipe) |>
       add_model(knn_tune) |>
       tune_grid(resamples = fruit_vfold, grid = k_vals) |>
       collect_metrics()

Now, let’s find the best value of the number of neighbors.

First, from knn_results, filter for accuracy from the .metric column.

Assign your answer to an object called accuracies.

Next, create a line plot using the accuracies dataset with neighbors on the x-axis and the mean on the y-axis.

Assign your answer to an object called accuracy_versus_k.

#... <- knn_results |> 
#       filter(...)

#... <- ggplot(..., aes(x = ..., y = ...))+
#       geom_point() +
#       geom_line() +
#       labs(x = "Neighbors", y = "Accuracy Estimate") +
#       scale_x_continuous(breaks = seq(0, 14, by = 1)) +  # adjusting the x-axis
#       scale_y_continuous(limits = c(0.4, 1.0)) # adjusting the y-axis

Click for answer

accuracies <- knn_results |> 
       filter(.metric == "accuracy")

accuracy_versus_k <- ggplot(accuracies, aes(x = neighbors, y = mean))+
       geom_point() +
       geom_line() +
       labs(x = "Neighbors", y = "Accuracy Estimate") +
       scale_x_continuous(breaks = seq(0, 14, by = 1)) +  # adjusting the x-axis
       scale_y_continuous(limits = c(0.4, 1.0)) # adjusting the y-axis

accuracy_versus_k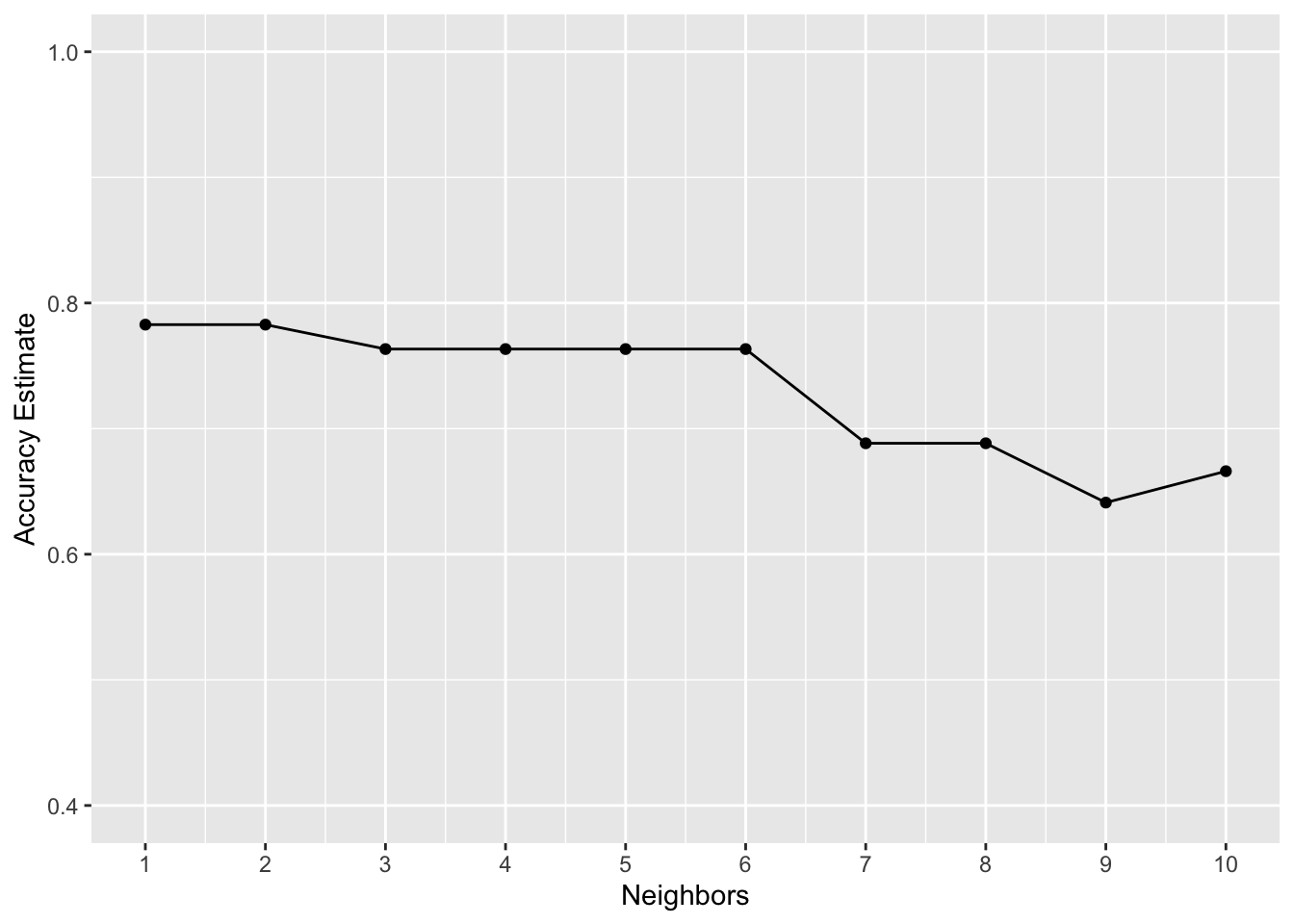

from the plot above, we can see that \(K = 2\), \(3\), or \(6\) provides the highest accuracy. Larger \(K\) values result in a reduced accuracy estimate. Remember: the values you see on this plot are estimates of the true accuracy of our classifier. Although the \(K = 2\), \(3\) or \(4\) value is higher than the others on this plot, that doesn’t mean the classifier is necessarily more accurate with this parameter value!

Great, now you have completed a full workflow analysis with cross-validation using the tidymodels package! For your information, we can choose any number of folds and typically, the more we use the better our accuracy estimate will be (lower standard error). However, more folds would mean a greater computation time. In practice, \(C\) is chosen to be either 5 or 10.

Assignment 5 (Total Marks:39)

Deadline: Friday Nov 17st, 11:59 p.m

1. What does tuning a parameter mean? Is it part of testing the model? Explain. [2pts]

2. Below is an R code segment that imports the tidymodels and discrim packages, in addition to loading the mobile_carrier_df dataset.

library(tidymodels)
library(discrim)

Attaching package: 'discrim'

The following object is masked from 'package:dials':

    smoothness

mobile_carrier_df <- 
  readRDS(url('https://gmubusinessanalytics.netlify.app/data/mobile_carrier_data.rds'))

The mobile_carrier_df dataframe holds data on customers from a nationwide mobile service provider in the U.S.

In this dataset, each row corresponds to a customer and indicates whether they terminated their service. The target variable is canceled_plan, which is categorical with ‘yes’ or ‘no’ as possible values. The features included provide details on the customers’ geographic location and their mobile phone usage patterns.

2.1 Please examine the dataset. Is there a need to convert the data type of the response variable? [1]

2.2 Construct a bar chart with ggplot2 to display the count of records per category in canceled_plan. Color the bars light blue and label the x and y axes appropriately. Apply the classic theme to your plot. [3]

2.3 Based on the graph, do you think this dataset is balanced? Explain your reseaoning briefly [1]

2.4 Is there any missing value in this dataset? [1]

2.5 using tidymodels,allocate 80% of the dataset to mobile_training for the training subset and 20% to mobile_testing for the testing subset. Ensure that the split maintains the category proportions within each subset. use set.seed(271). [2]

2.6 Create a recipe by using the formula below to include only numeric variables for the predictors and canceled_plan as the response variable. Use proper functions to scale and center the numeric variables.[3]

my_formula <- formula(canceled_plan~ number_vmail_messages+total_day_minutes+total_day_calls+total_eve_minutes+total_eve_calls+total_night_minutes+total_night_calls+total_intl_minutes+total_intl_calls+number_customer_service_calls)

2.7 Create 6 cross validation fold for hyper parameter tuning, name it mobile_folds. use the same seed; set.seed(271). [1]

2.8 Specify your KNN model, set the proper parameter that allows tuning in your downstream analysis.[2]

2.9 Create a workflow by combing your model and recipe.[2]

2.10 Create a tibble of \(k\) values called k_vals that contains 10, 15, 25, 45, 60, 80, 100.[1]

2.11 Now, complete your workflow by doing grid search (tune_grid()) to perform hyperparameter tuning using k_vals and mobile_folds. set seed to 314.[2]

2.12 Provide a table of the accuracy for each \(k\).[2]

2.13 which \(k\) would you choose to be the final hyperparameter for your model? Explain your reasons. [2]

2.14 Now, create a another KNN specification (knn25_spec) and a seperate workflow that use best number of neighbors from prevoius to fit the model.set seed to 176.[3]

2.15 Predict the test data by the fitted model.Add the true class to the predicted dataframe.[2]

2.16 Provide a confusion matrix to evaluate the performance of your model.[1]

2.17 Calculate the Precision and recall for this classifier.[2]

3. Describe advantages and disadvantages of the k-nearest neighbour classification algorithm.[3 pts]
4. What does overfitting and underfitiing mean in machine learning? [3 pts]

General formating expectations

Code formatting. Code must appear within an R chunk with the appropriate chunk options (e.g. echo = TRUE unless otherwise specified)

```{r, echo=TRUE}
# this is some simple addition
x <- 2 + 4
x
```

[1] 6

or inline with text:

# inline R code:
This is some text with inline R code: `r mean(c(1, 2, 3, 4, 5))`.

which renders to: This is some text with inline R code: 3.

Text formatting Narrative and word answers should be typeset using regular text (as opposed to using using comments (preceded by #) within an R chunk. The use of of markdown formatting to improve readability is encouraged. Simple examples include:

• headers (second-level headers are preceded by ##)
• italics (*italics* or _italics_),
• bold (**bold**),
• typewritter text (`typewritter`)

Labels all HTML documents should satisfy the following criteria:

• assignments should be named assignment<x>_<y>.html where <x> is replaced by the assignment number and ` is replaced by your student number
• Your full name, student number, assignment number, and course number should appear somewhere near the top of the rendered document
• Questions should be labeled either by the use of headers or numbered lists.

Important

Submissions in any other format (e.g. Rmd, word document) will incur a 20% penalty.