Lab Tutorial 5

Author

Ladan Tazik

Published

October 21, 2023

Summary:

Towards the end of the lab, you will find a set of assignment exercises (Assignment 4). These assignments are to be completed and submitted on Canvas.

Lab 05

After completing this week’s tutorial work, you will be able to:

Recognize situations where a simple classifier would be appropriate for making predictions.
Explain the k-nearest neighbor classification algorithm.
Interpret the output of a classifier.
Compute, by hand, the distance between points when there are two explanatory variables/predictors.
Perform k-nearest neighbour classification in R using tidymodels to predict the class of a single new observation.

### Run this cell before continuing. 
library(tidyverse)
library(repr)
library(tidymodels)
options(repr.matrix.max.rows = 6)

Classification for Breast Cancer dataset

Breast cancer can be diagnosed by performing a biopsy, a process where tissue is removed from the body and examined for the presence of disease. Traditionally these procedures were quite invasive; modern methods such as fine needle aspiration, used to collect the present data set, extract only a small amount of tissue and are less invasive.

Based on a digital image of each breast tissue sample collected for this data set, ten different variables were measured for each cell nucleus in the image (items 3–12 of the list of variables below), and then the mean for each variable across the nuclei was recorded. Each image additionally was given a unique ID and a diagnosis by a physician. Therefore, the total set of variables per image in this data set is:

ID: identification number
Class: the diagnosis (M = malignant or B = benign)
Radius: the mean of distances from center to points on the perimeter
Texture: the standard deviation of gray-scale values
Perimeter: the length of the surrounding contour
Area: the area inside the contour
Smoothness: the local variation in radius lengths
Compactness: the ratio of squared perimeter and area
Concavity: severity of concave portions of the contour
Concave Points: the number of concave portions of the contour
Symmetry: how similar the nucleus is when mirrored
Fractal Dimension: a measurement of how “rough” the perimeter is.

Suppose we have past data of cancer tumour cell diagnosis labelled “benign” and “malignant”. Do you think a new cell with Concavity = 3.3 and Perimeter = 0.2 would be malignant? How did you decide?

Question 0.1: What kind of data analysis question is this?

descriptive
exploratory
predictive
inferential
causal

Click for answer

Predictive

The breast cancer data for the next part have been standardized (centred and scaled) for you already. We will implement these steps later, but for now, know the data has been standardized. Therefore the variables are unitless and hence why we have zero and negative values for variables like Radius.

Question 0.2

Read the clean-wdbc-data.csv file (found in the data module on Canvas) using the read_csv() function into the notebook and store it as a data frame. Name it cancer.

Click for answer

cancer <- read_csv("https://irene.vrbik.ok.ubc.ca/data/clean-wdbc-data.csv")

Rows: 569 Columns: 12
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr  (1): Class
dbl (11): ID, Radius, Texture, Perimeter, Area, Smoothness, Compactness, Con...

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

Click for answer

glimpse(cancer)

Rows: 569
Columns: 12
$ ID                <dbl> 842302, 842517, 84300903, 84348301, 84358402, 843786…
$ Class             <chr> "M", "M", "M", "M", "M", "M", "M", "M", "M", "M", "M…
$ Radius            <dbl> 1.8850310, 1.8043398, 1.5105411, -0.2812170, 1.29743…
$ Texture           <dbl> -1.35809849, -0.36887865, -0.02395331, 0.13386631, -…
$ Perimeter         <dbl> 2.30157548, 1.53377643, 1.34629062, -0.24971958, 1.3…
$ Area              <dbl> 1.999478159, 1.888827020, 1.455004298, -0.549537693,…
$ Smoothness        <dbl> 1.306536657, -0.375281748, 0.526943750, 3.391290721,…
$ Compactness       <dbl> 2.61436466, -0.43006581, 1.08198014, 3.88997467, -0.…
$ Concavity         <dbl> 2.10767182, -0.14661996, 0.85422232, 1.98783917, 0.6…
$ Concave_points    <dbl> 2.29405760, 1.08612862, 1.95328166, 2.17387323, 0.72…
$ Symmetry          <dbl> 2.7482041, -0.2436753, 1.1512420, 6.0407261, -0.8675…
$ Fractal_dimension <dbl> 1.93531174, 0.28094279, 0.20121416, 4.93067187, -0.3…

Question 0.3 True or False:

After looking at the first six rows of the cancer data fame, suppose we asked you to predict the variable “area” for a new observation. Is this a classification problem?

Note

Look at the values in the Area column - are they categorical? Remember, classification problems involve predicting class labels for categorical data.

We will be treating Class as a categorical variable, so Let’s convert it into a factor using the as_factor() function.

Click for answer

cancer <- cancer |>
  mutate(Class = as_factor(Class))

Question 0.5 Create a scatterplot of the data with Symmetry on the x-axis and Radius on the y-axis. Modify your aesthetics by colouring for Class. As you create this plot, ensure you follow the guidelines for creating effectxfruiive visualizations. In particular, note on the plot axes whether the data is standardized or not. Assign your plot to an object called cancer_plot.

Click for answer

cancer_plot <- cancer |>
               ggplot(aes(x = Symmetry, y = Radius, color = Class)) +
               geom_point()+
                theme_minimal()
cancer_plot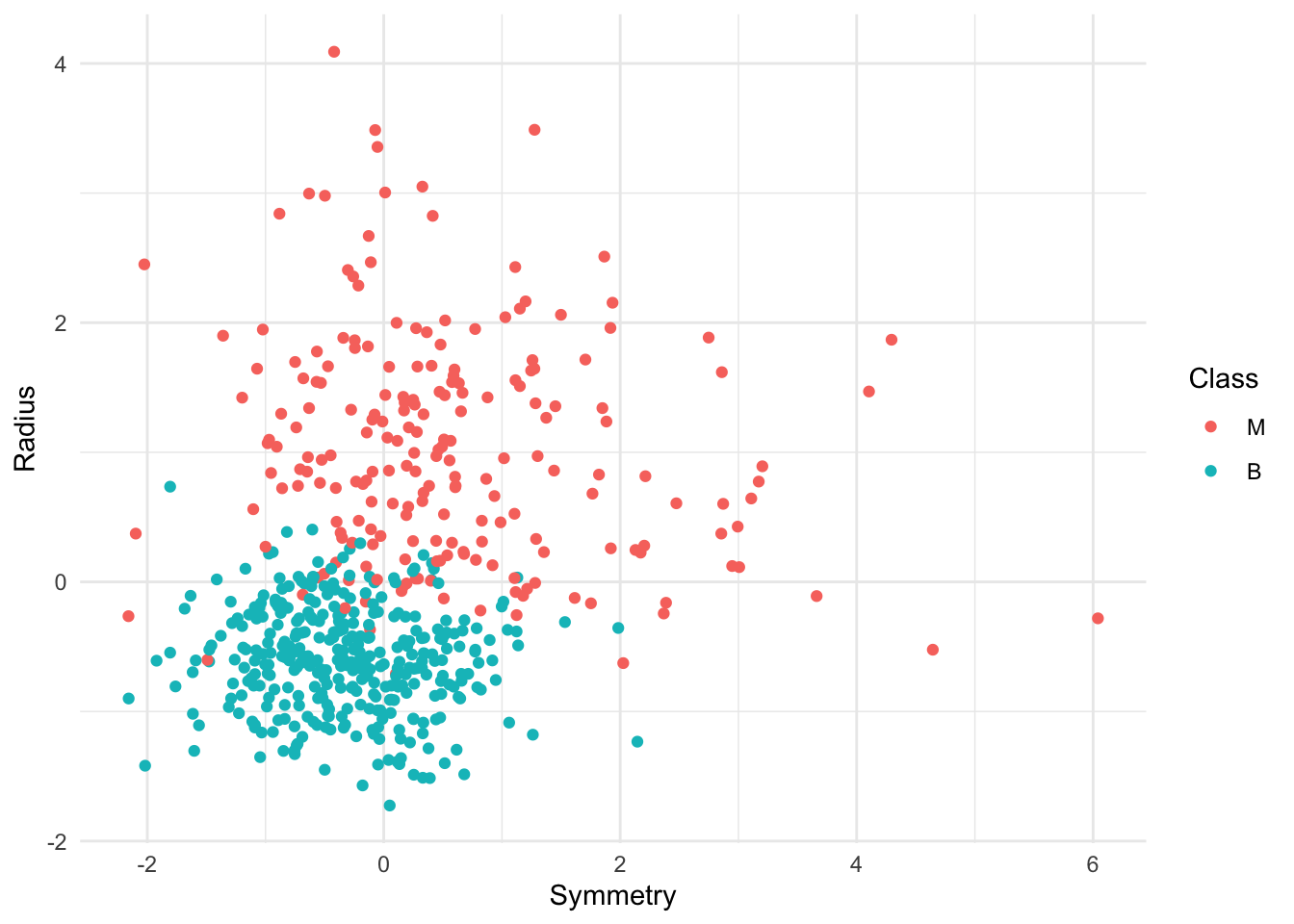

Just by looking at the scatterplot above, how would you classify an observation with Symmetry = 1 and Radius = 1 (Benign or Malignant)?

Note

Looking at the location of (1,1) the data point is Malignant.

K-nearest neighbours classification

Predict the label / class for a new observation using the K closest points from our dataset.

The following steps are the backbone of KNN classification method:

Compute the distance between the new observation and each observation in our training set.Recall from your reading, the training dataset is the sample of data used to fit the model.
Sort the data in ascending order according to the distances
Choose the top K rows as “neighbours”
Assign the label/class for the new observation based on majority votes from “neighbors”.

1. Compute Distances

Let’s compute the distance between the first and second observation in the breast cancer dataset using the explanatory variables/predictors Symmetry and Radius. Recall we can calculate the distance between two points using the following formula:

\[Distance = \sqrt{(a_x -b_x)^2 + (a_y - b_y)^2}\] Question 1.1

First, extract the coordinates for the two observations and assign them to objects called:

ax (Symmetry value for the first row)
ay (Radius value for the first row)
bx (Symmetry value for the second row)
by (Radius value for the second row).

Scaffolding for ax is given. > Note we are using the function pull() because we want the numeric value (and object) as our output rather than a tibble type object so we can do calculations later on. You can verify the object type in R with the class() function. Check the class of ax with and without the pull() function and see what you get! Use ?pull to learn more.

# ax <- slice(cancer, 1) |>     pull(Symmetry)

Click for answer

ax <- slice(cancer, 1) |>     pull(Symmetry)

ay <- slice(cancer, 1) |>     pull(Radius)

bx <- slice(cancer, 2) |>     pull(Symmetry)

by <- slice(cancer, 2) |>     pull(Radius)

Question 1.2 Plug the coordinates into the distance equation. Assign your answer to an object called answer1.2.

#... <- sqrt((... - ...)^... + (... - ...)^...)

Click for answer

answer1.2 <- sqrt(( ax-bx )^2 + (ay - by)^2)

Question 1.3

Now we’ll do the same thing with 3 explanatory variables/predictors: Symmetry, Radius and Concavity. Again, use the first two rows in the data set as the points you are calculating the distance between (point \(a\) is row 1, and point \(b\) is row 2).

Find the coordinates for the third variable (Concavity) and assign them to objects called az and bz. Use the scaffolding given in Question 1.1 as a guide.

Click for answer

az <- slice(cancer, 1) |>     pull(Concavity)

bz <- slice(cancer, 2) |>     pull(Concavity)

Question 1.4

Again, calculate the distance between the first and second observation in the breast cancer dataset using 3 explanatory variables/predictors: Symmetry, Radius and Concavity.

Assign your answer to an object called answer1.4. Use the scaffolding given to calculate answer1.2 as a guide.

Click for answer

answer1.4 <- sqrt((ax-bx)^2 + (ay - by)^2 +(az-bz)^2)

Question 1.5

Let’s do this without explicitly making coordinate variables!

Create a vector of the coordinates for each point. Name one vector point_a and the other vector point_b. Within the vector, the order of coordinates should be: Symmetry, Radius, Concavity.

Fill in the ... in the cell below.

Here will use select and as.numeric instead of pull because we need to get the numeric values of 3 columns. pull, that we used previously, only works to extract the numeric values from a single column.

# This is only the scaffolding for one vector 
# You need to make another one for row number 2!

#... <- slice(cancer, 1) |>
#    select(..., Radius, ...) |>
#    as.numeric()

Click for answer

point_a <- slice(cancer, 1) |> select(Symmetry, Radius, Concavity) |> as.numeric()

point_b <- slice(cancer, 2) |> select(Symmetry, Radius, Concavity) |> as.numeric()

Question 1.6

Compute the squared differences between the two vectors, point_a and point_b. The result should be a vector of length 3 named dif_square. Hint: ^ is the exponent symbol in R.

Click for answer

dif_square <- (point_a - point_b)^2

Question 1.6.1

Sum the squared differences between the two vectors, point_a and point_b. The result should be a single number named dif_sum.

Hint: the sum function in R returns the sum of the elements of a vector

Click for answer

dif_sum <- sum(dif_square)

Question 1.6.2

Square root the sum of your squared differences. The result should be a double named root_dif_sum.

Click for answer

root_dif_sum <- sqrt(dif_sum)

Question 1.6.3

If we have more than a few points, calculating distances as we did in the previous questions is VERY tedious. Let’s use the dist() function to find the distance between the first and second observation in the breast cancer dataset using Symmetry, Radius and Concavity.

Fill in the ... in the cell below.

Assign your answer to an object called dist_cancer_two_rows.

# ... <- cancer  |> 
#    slice(1,2)  |> 
#    select(..., ..., Concavity)  |> 
#    dist()
# your code

Click for answer

dist_cancer_two_rows <- cancer |>
  slice(1,2)|>
  select(Symmetry, Radius, Concavity)|>
  dist()

Question 1.6.4 True or False:

Compare answer1.4, root_dif_sum, and dist_cancer_two_rows.

Are they all the same value?

Note: We can go beyond 3 predictors

For two observations \(u, v\), each with \(m\) variables (columns) labelled \(1, \dots, m\),

\(\text{Distance} = \sqrt{(u_1-v_1)^2 + (u_2-v_2)^2 + \dots + (u_m - v_m)^2}\)

Aside from that, it’s the same algorithm!

2.A Simple Example Done Manually

Question 2.0.0

Let’s take a random sample of 5 observations from the breast cancer dataset using the sample_n function. To make this random sample reproducible, we will use set.seed(20). This means that the random number generator will start at the same point each time when we run the code and we will always get back the same random samples.

We will focus on the predictors Symmetry and Radius only. Thus, we will need to select the columns Symmetry and Radius and Class. Save these 5 rows and 3 columns to a data frame named small_sample.

Fill in the ... in the scaffolding provided below.

#set.seed(20)                           
#... <- sample_n(cancer, 5) |>  
#    select(...)

Click for answer

set.seed(20)                     

small_sample<- sample_n(cancer, 5) |> select(Symmetry, Radius, Class)

Question 2.0.1

Finally, create a scatter plot where Symmetry is on the x-axis, and Radius is on the y-axis. Color the points by Class. Name your plot small_sample_plot.

Fill in the ... in the scaffolding provided below.

As you create this plot, ensure you follow the guidelines for creating effective visualizations. In particular, note on the plot axes whether the data is standardized or not.

#... <- ...|>   
#    ggplot(...) + 
#        geom_...() +
#        ...

Click for answer

set.seed(20)
small_sample_plot <- small_sample |> 
  ggplot(aes(x = Symmetry, y = Radius, color = Class)) +
  geom_point()+
  theme_minimal()
small_sample_plot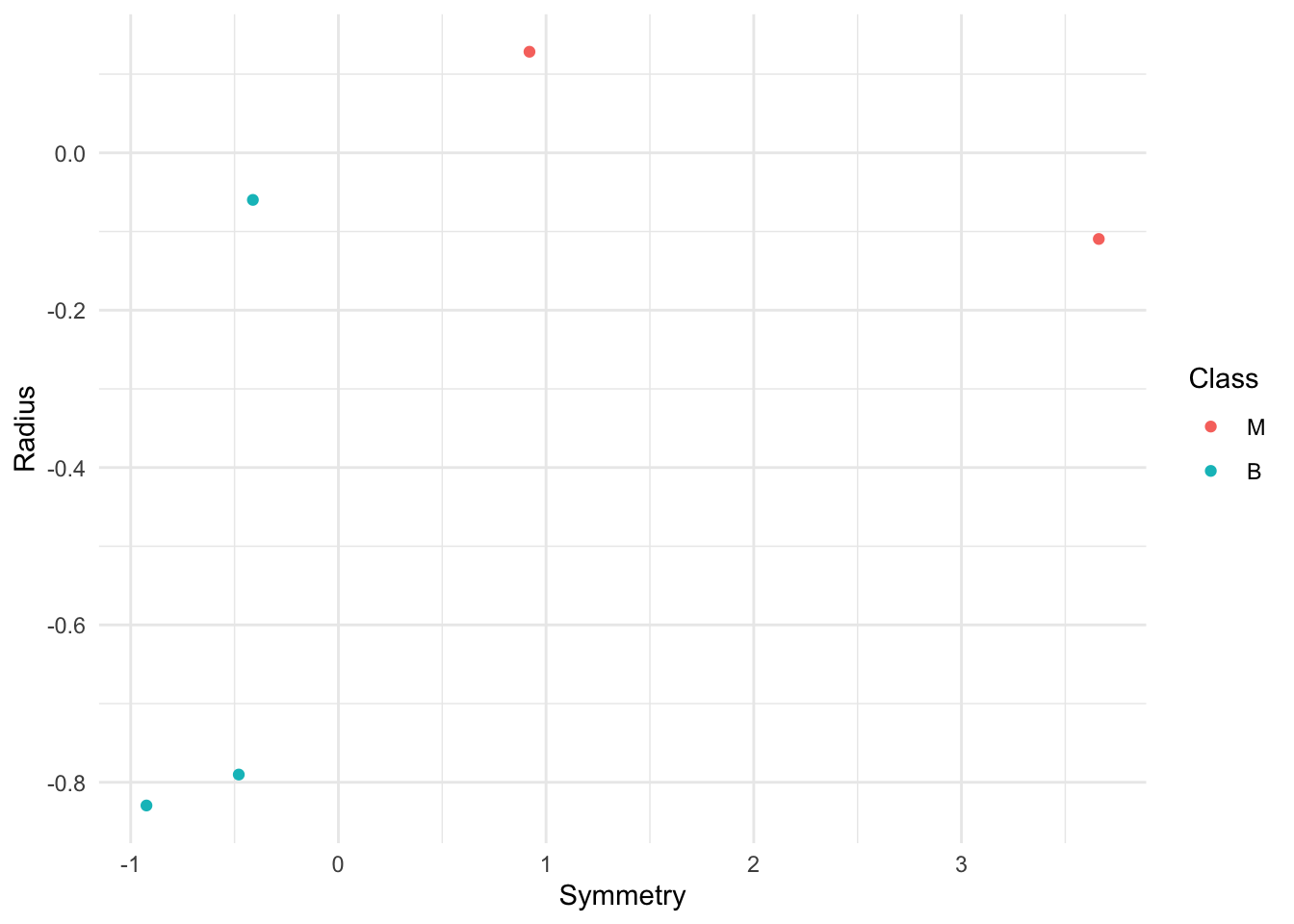

Question 2.1

Suppose we are interested in classifying a new observation with Symmetry = 0.5 and Radius = 0, but unknown Class. Using the small_sample data frame, add another row with Symmetry = 0.5, Radius = 0, and Class = "unknown".

Fill in the ... in the scaffolding provided below.

Assign your answer to an object called newData.

#... <- ... |>
#    add_row(Symmetry = ..., ... = 0, Class = ...)

Click for answer

newData <- small_sample|> add_row(Symmetry = 0.5, Radius = 0, Class = "unknown")

Question 2.2

Compute the distance between each pair of the 6 observations in the newData dataframe using the dist() function based on two variables: Symmetry and Radius. Fill in the ... in the scaffolding provided below.

Assign your answer to an object called dist_matrix.

# ... <- newData |>
#    select(..., ...) |> 
#    ...() |>                   
#    as.matrix()

Click for answer

dist_matrix <- newData |>
  slice(1:6) |>
  select(Symmetry, Radius) |>
  dist() |>
  as.matrix()

Question 2.3 Multiple Choice:

In the table above, the row and column numbers reflect the row number from the data frame the dist function was applied to. Thus numbers 1 - 5 were the points/observations from rows 1 - 5 in the small_sample data frame. Row 6 was the new observation that we do not know the diagnosis class for. The values in dist_matrix are the distances between the points of the row and column number. For example, the distance between the point 2 and point 4 is 4.196683. And the distance between point 3 and point 3 (the same point) is 0.

Which observation is the nearest to our new point?

Click for answer

order(dist_matrix[6, c(1:5)]) #exclude the last column since it's the distance with itself

# The smallest value is at 5 so observation 5

Question 2.4 Multiple Choice:

Use the K-nearest neighbour classification algorithm with K = 1 to classify the new observation using your answers to Questions 2.2 & 2.3. Is the new data point predicted to be benign or malignant?

Click for answer

small_sample$Class[5]  #  look at the class of row 5

Question 2.5 Multiple Choice:

Using your answers to Questions 2.2 & 2.3, what are the three closest observations to your new point?

A. 1, 3, 2

B. 5, 1, 4

C. 5, 2, 4

D. 3, 4, 2

Click for answer

#B

Question 2.6 Multiple Choice:

We will now use the K-nearest neighbour classification algorithm with K = 3 to classify the new observation using your answers to Questions 2.2 & 2.3. Is the new data point predicted to be benign or malignant?

Click for answer

small_sample$Class[c(5,1,4)]  #

[1] M B B
Levels: M B

Click for answer

# 2/3 is B so the predicted class is B

Question 2.7

Compare your answers in 2.4 and 2.6. Are they the same?

Standardizing Data

When using K-nearest neighbour classification, the scale of each variable (i.e., its size and range of values) matters. Since the classifier predicts classes by identifying observations that are nearest to it, any variables that have a large scale will have a much larger effect than variables with a small scale. But just because a variable has a large scale doesn’t mean that it is more important for making accurate predictions. - For example, suppose you have a data set with two attributes, height (in feet) and weight (in pounds).

\[distance1 = \sqrt{(202 - 200)^2 + (6 - 6)^2} = 2\]

\[distance2 = \sqrt{(200 - 200)^2 + (8 - 6)^2} = 2\]

Here if we calculate the distance we get 2 in both cases! A difference of 2 pounds is not that big, but a different in 2 feet is a lot.

So how we adjust that? What if one variable is much larger than the other?

Standardize: shift (center) and scale so that the average is 0 and the standard deviation is 1.

When all variables in a data set have a mean (center) of 0 and a standard deviation (scale) of 1, we say that the data have been standardized. standardizing the data can change things in an important way when we are using predictive algorithms. As a rule of thumb, standardizing your data should be a part of the preprocessing you do before any predictive modelling / analysis.

Introduction to the `tidymodels` package in R

Now that we understand how K-nearest neighbours (k-nn) classification works, let’s get familar with the tidymodels R package. The benefit of using tidymodels is that it will keep our code simple, readable and accurate. Coding less and in a tidier format means that there is less chance for errors to occur.

tidymodels is a collection of packages and handles computing distances, standardization, balancing, and prediction for us!

Remember to install and load the the package tidymodels.

library(tidyverse)
library(tidymodels)
options(repr.matrix.max.rows = 6)

1. Preprocess the data

In tidymodels, the recipes package is named after cooking terms.

Make a recipe to specify the predictors/response and preprocess the data.recipe(): Main argument in the formula.

Arguments: - formula - data

prep() & bake(): you can also prep and bake a recipe to see what the preprocessing does!

More specifically;

The prep() function computes everything so that the preprocessing steps can be executed
The bake() function takes a recipe and applies it to data and returns data

visit https://recipes.tidymodels.org/reference/index.html to see all the preprocessing steps.

Note: If you want to extract the pre-processed dataset: you can prep() and bake() but extracting the pre-processed data isn’t necessary for the data analysis pipeline, since this will be done under the hood when the model is fit. We talk more about fitting the model in a bit.

We’ll again focus on Radius and Symmetry as the two predictors. This time, we would like to predict the class of a new observation with Symmetry = 1 and Radius = 0. This one is a bit tricky to do visually from the plot above, and so is a motivating example for us to compute the prediction using k-nn with the tidymodels package. Let’s use K = 7.

Fill in ... below for classifying the class of a tumor based on Symmetry and Radius variables.

# Standardize the cancer data
tumor_recipe <- recipe(... ~ ... + ..., data=cancer) |>
                 step_center(...) |>
                 step_scale(...) |>
                 prep() #just in case you want to save the scaled data
tumor_recipe

first argument “Model formula”
Left hand side of ~: “response” / thing we are trying to predict (can selectively remove, but another step)
Right hand side: whatever columns you want to use as predictors (could use a . to use everything as a predictor)
second argument: data frame
pre-processing steps to standardize data

Click for answer

tumor_recipe <- recipe(Class ~ Symmetry + Radius, data=cancer) |>
                  step_center(all_predictors()) |>
                  step_scale(all_predictors()) |>
                  prep()
tumor_recipe

── Recipe ──────────────────────────────────────────────────────────────────────

── Inputs

Number of variables by role

outcome:   1
predictor: 2

── Training information

Training data contained 569 data points and no incomplete rows.

── Operations

• Centering for: Symmetry, Radius | Trained

• Scaling for: Symmetry, Radius | Trained

You can find a full set of all the steps and variable selection functions on the recipe reference page

2. Build a model specification (`model_spec`) to specify the model and training algorithm

model type: kind of model you want to fit
arguments: model parameter values
engine: underlying package the model should come from
mode: type of prediction (some packages can do both classification and regression)

Question 3.1

Create a model specification for K-nearest neighbours classification by using the nearest_neighbor() function. Specify that we want to set k = 7 and use the straight-line distance. Furthermore, specify the computational engine to be "kknn" for training the model with the set_engine() function. Finally, identify that this is a classification problem with the set_mode() function.

Name your model specification knn_spec.

#... <- nearest_neighbor(weight_func = ..., neighbors = ...) |>
#       set_engine(...) |>
#       set_mode(...)

Click for answer

knn_spec <- nearest_neighbor(weight_func = "gaussian", neighbors = 7) |>
      set_engine("kknn") |>
       set_mode("classification")

#or
#knn_spec <- nearest_neighbor(mode = "classification", engine = "kknn", weight_func = "gaussian", neighbors = 7)

3. Put them together in a workflow and then `fit` it

Question 3.2

To train the model on the breast cancer dataset, pass knn_spec and the cancer dataset to the fit() function. Specify Class as your target variable and the Symmetry and Radius variables as your predictors. Name your fitted model as knn_fit.

# ... <- ... |> 
#        fit(... ~ Symmetry + ..., data = ...)

Click for answer

knn_fit <- knn_spec |> 
        fit(Class ~ Symmetry + Radius, data = cancer)

4. Predict a new class label using `predict`

Question 4.1

Now we will make our prediction on the Class of a new observation with a Symmetry of 1 and a Radius of 0. First, create a tibble with these variables and values and call it new_obs. Next, use the predict() function to obtain our prediction by passing knn_fit and new_obs to it. Name your predicted class as class_prediction.

#... <- tibble(... = 1,... = 0)
#... <- predict(..., ...)

Click for answer

new_obs <- tibble(Symmetry = 1,Radius = 0)
class_prediction <- predict(knn_fit, new_obs)
class_prediction

# A tibble: 1 × 1
  .pred_class
  <fct>      
1 M

Question 4.2

Let’s perform K-nearest neighbour classification again, but with three predictors. Use the tidymodels package and K = 7 to classify a new observation where we measure Symmetry = 1, Radius = 0 and Concavity = 1.

Pass the same knn_spec from before to fit, but this time specify Symmetry, Radius, and Concavity as the predictors. Store the output in knn_fit_2.
store the new observation values in an object called new_obs_2
store the output of predict in an object called class_prediction_2

Click for answer

knn_fit2 <- knn_spec |> 
        fit(Class ~ Symmetry + Radius + Concavity, data = cancer)

new_obs2 <- tibble(Symmetry = 1,Radius = 0, Concavity = 1)
class_prediction_2 <- predict(knn_fit2, new_obs2)
class_prediction_2

# A tibble: 1 × 1
  .pred_class
  <fct>      
1 M

We may want to use our recipe across several steps as we train and test our model. To simplify this process, we can use a model workflow, which pairs a model and recipe together

tumor_workflow <- workflow() |>
    add_recipe(...) |>
    add_model(...)

tumor_fit <- ... |>
    fit(data=cancer)

tumor_workflow

Click for answer

tumor_workflow <- workflow() |>
    add_recipe(tumor_recipe) |>
    add_model(knn_spec)

tumor_fit <- tumor_workflow |>
    fit(data=cancer)

Assignment 4

Deadline: Wednesday Nov 1st, 11:59 p.m

Before applying k-nearest neighbour to a classification task, we need to scale the data. What is the purpose of this step? [1pt]
1. To help speed up the knn algorithm.
2. To convert all data observations to numeric values.
3. To ensure all data observations will be on a comparable scale and contribute equal shares to the calculation of the distance between points.
4. None of the above.
Fruit Dataset

In the agricultural industry, cleaning, sorting, grading, and packaging food products are all necessary tasks in the post-harvest process. Products are classified based on appearance, size and shape, attributes which helps determine the quality of the food. Sorting can be done by humans, but it is tedious and time consuming. Automatic sorting could help save time and money. Images of the food products are captured and analysed to determine visual characteristics.

The dataset contains observations of fruit described with four features 1- mass (in g) 2- width (in cm) 3- height (in cm) 4- color score (on a scale from 0 - 1).

2.1- Load the file, fruit_data.csv, into your workspace.mutate() the fruit_name column such that it is a factor using the as_factor() function. Assign your data to an object called fruit_data. [2pt]

2.2- Which of the columns should we treat as categorical variables?[1pt]

Fruit label, width, fruit subtype
Fruit name, color score, height
Fruit label, fruit subtype, fruit name
Color score, mass, width

2.3- Run the cell below, and find the nearest neighbour based on mass and width to the first observation just by looking at the scatterplot (the first observation has been circled for you). [1]

# Run this cell. 
options(repr.plot.width=10, repr.plot.height=7)
point1 <- c(192, 8.4)
point2 <- c(180, 8)
point44 <- c(194, 7.2)

fruit_data |>  
    ggplot(aes(x=mass, 
               y= width, 
               colour = fruit_name)) +
        labs(x = "Mass (grams)",
             y = "Width (cm)",
            colour = 'Name of the Fruit') +
        geom_point(size = 2.5) +
        annotate("path", 
                 x=point1[1] + 5*cos(seq(0,2*pi,length.out=100)),
                 y=point1[2] + 0.1*sin(seq(0,2*pi,length.out=100))) +
        annotate("text", x = 183, y =  8.5, label = "1", size = 8) + 
        theme(text = element_text(size = 20))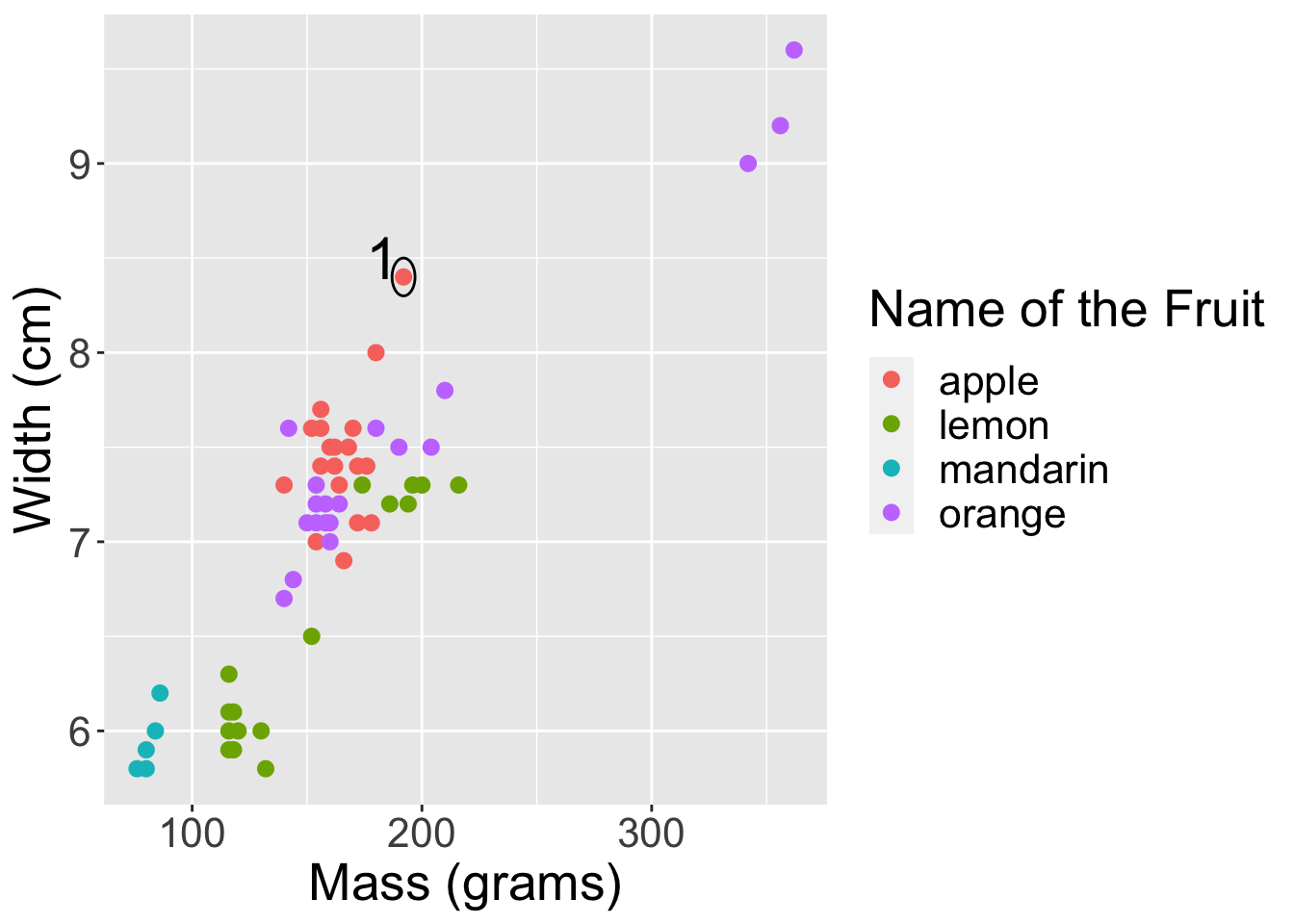

Based on the graph generated, what is the fruit_name of the closest data point to the one circled?

apple
lemon
mandarin
orange

2.3 Using mass and width, calculate the distance between the first observation and the second observation.Assign your answer to an object called fruit_dist_2.[1]

2.4 Calculate the distance between the first and the the 44th observation in the fruit dataset using the mass and width variables. Assign your answer to an object called fruit_dist_44.[1]

2.5 these three observations are circled on the plot from earlier.

options(repr.plot.width = 10, repr.plot.height = 7)

# Run this cell. 
point1 <- c(192, 8.4)
point2 <- c(180, 8)
point44 <- c(194, 7.2)

fruit_data |>
    ggplot(aes(x = mass, 
               y = width, 
               colour = fruit_name)) +
        labs(x = "Mass (grams)",
             y = "Width (cm)",
            colour = 'Name of the Fruit') +
        geom_point(size = 2.5) +
        theme(text = element_text(size = 20)) +
        annotate("path", 
                 x=point1[1] + 5*cos(seq(0,2*pi,length.out=100)),
                 y=point1[2] + 0.1*sin(seq(0,2*pi,length.out=100))) +
        annotate("text", x = 183, y =  8.5, label = "1", size = 8) +
        annotate("path",
                 x=point2[1] + 5*cos(seq(0,2*pi,length.out=100)),
                 y=point2[2] + 0.1*sin(seq(0,2*pi,length.out=100))) +
        annotate("text", x = 169, y =  8.1, label = "2", size = 8) +
        annotate("path",
                 x=point44[1] + 5*cos(seq(0,2*pi,length.out=100)),
                 y=point44[2]+0.1*sin(seq(0,2*pi,length.out=100))) +
        annotate("text", x = 204, y =  7.1, label = "44", size = 8)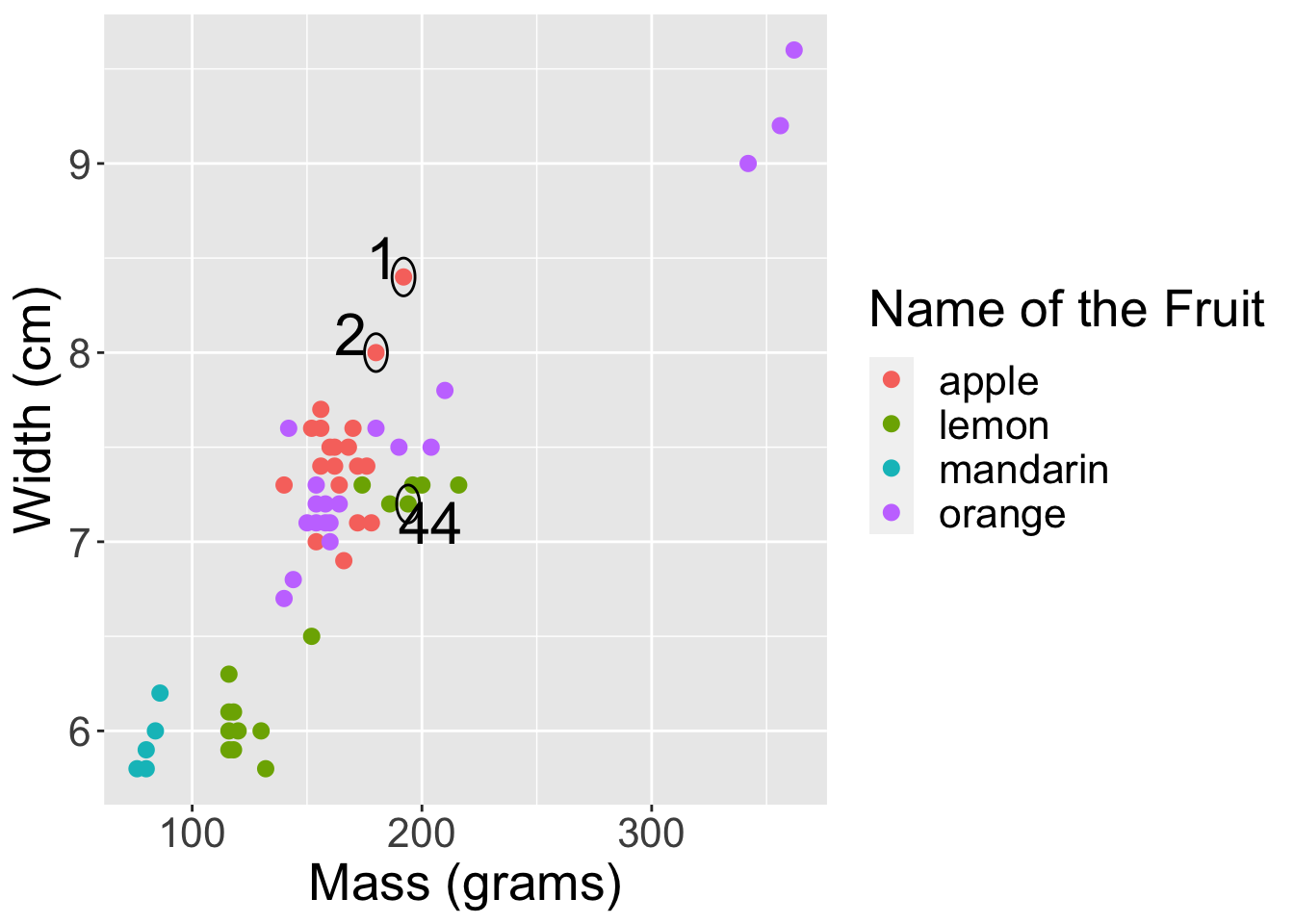

The distance between the first and second observation is 12.01 and the distance between the first and 44th observation is 2.33. By the formula, observation 1 and 44 are closer, however, if we look at the scatterplot the distance of the first observation to the second observation appears closer than to the 44th observation.

Which of the following statements is correct? [1]

A. A difference of 12 g in mass between observation 1 and 2 is large compared to a difference of 1.2 cm in width between observation 1 and 44. Consequently, mass will drive the classification results, and width will have less of an effect.

B. If we measured mass in kilograms, then we’d get different nearest neighbours.

C. We should standardize the data so that all variables will be on a comparable scale.

D. All of the above.

2.6 Create a tidymodels recipe to standardize (i.e., center and scale) all of the variables in the fruit dataset. Specify your recipe with class variable fruit_name and predictors mass, width, height, and color_score. Name the recipe fruit_data_recipe.[3]

# Set the seed. Don't remove this!
set.seed(9999) 
#your solution

2.6.1 Use bake to apply recipe to your original data. Save the scaled data to scaled_fruit_data. [1]

2.7 Let’s repeat Question 2.3 and 2.4 with the scaled variables:

2.7.1 calculate the distance with the scaled mass and width variables between observations 1 and 2.[1]

2.7.2 calculate the distances with the scaled mass and width variables between observations 1 and 44. [1]

After you do this, think about how these distances compared to the distances you computed in Question 1.2 and 1.3 for the same points.

Assign your answers to objects called distance_2 and distance_44 respectively.

2.8 Make a scatterplot of scaled mass on the horizontal axis and scaled color score on the vertical axis to show this relationship for each fruit name. (hint: use faceting). Ensure proper labeling for the x and y axes and color the data points using ‘lightblue’.” [4]

Assign your plot to an object called fruit_plot.

2.9 Make another scatterplot of scaled mass on the horizontal axis and scaled color score on the vertical axis and color the datapoints based of their fruit name. [1]

Assign your plot to an object called fruit_plot2.

2.10 Suppose we have a new observation in the fruit dataset with scaled mass 0.5 and scaled color score 0.5. Just by looking at the scatterplot, how would you classify this observation using K-nearest neighbours if you use K = 3? Explain how you arrived at your answer. [1]

2.11 Use the tidymodels package to predict fruit_name for another new observation. The new observation we are interested in has mass 150g and color score 0.73.

First, create the K-nearest neighbour model specification. Specify that we want \(K=5\) neighbors, set_engine to be "kknn", and that each neighboring point should have the same weight when voting. Name this model specification as my_knn.

Then create a new recipe named fruit_data_recipe_2 that centers and scales the predictors, but only uses mass and color_score as predictors.

Combine this with your recipe from before in a workflow, and fit to the fruit_data dataset.

Name the fitted model fruit_fit. [8]

Use set.seed(9999) at first

2.12 Create a new tibble where mass = 150 and color_score = 0.73 and call it new_fruit. Then, pass fruit_fit and new_fruit to the predict function to predict the class for the new fruit observation. Save your prediction to an object named fruit_predicted.

Wheat Seed Dataset

X-ray images can be used to analyze and sort seeds. In this data set, we have 7 measurements from x-ray images from 3 varieties of wheat seeds (Kama, Rosa and Canadian). The data set is available here: https://archive.ics.uci.edu/ml/machine-learning-databases/00236/seeds_dataset.txt

The seven measurements were taken below for each wheat kernel: 1. area A, 2. perimeter P, 3. compactness C = 4piA/P^2, 4. length of kernel, 5. width of kernel, 6. asymmetry coefficient 7. length of kernel groove.

The last column in the data set is the variety label. The mapping for the numbers to varieties is listed below:

1 == Kama
2 == Rosa
3 == Canadian

3.1 Download the dataset directly from this URL using the read_table2() function. This function is especially useful when the columns are separated by one or more white spaces. Please take note that the dataset lacks column names, so be sure to set the appropriate parameter to handle this. [1]

3.2 We provide a string list of column names from the information above. Assign it to the dataset so each column gets it’s name. [1]

mycol_names <- c("area", "perimeter", "compactness", "length", "width", "asymmetry_coefficient", "groove_length", "label")

3.3 Explore the dataset and determine the number of observations within each variety label. Be sure to enforce type correction for the variety label column. [2]

# Set the seed. Don't remove this!
set.seed(9999) 

#This is the new observation to predict
new_seed <- tibble(area = 12.1,
                        perimeter = 14.2,
                        compactness = 0.9,
                        length = 4.9,
                        width = 2.8,
                        asymmetry_coefficient = 3.0, 
                        groove_length = 5.1)

3.4 Similar to the question before, by using KNN with K = 4 and using all the features as predictors, What is the predicted class for the new_seed observation?( preprocess data as needed) [8]

A. Kama

B. Rosa

C. Canadian

General formating expectations

Code formatting (1 point). Code must appear within an R chunk with the appropriate chunk options (e.g. echo = TRUE unless otherwise specified)

```{r, echo=TRUE}
# this is some simple addition
x <- 2 + 4
x
```

[1] 6

or inline with text:

# inline R code:
This is some text with inline R code: `r mean(c(1, 2, 3, 4, 5))`.

which renders to: This is some text with inline R code: 3.

Text formatting (1 point) Narrative and word answers should be typeset using regular text (as opposed to using using comments (preceded by #) within an R chunk. The use of of markdown formatting to improve readability is encouraged. Simple examples include:

headers (second-level headers are preceded by ##)
italics (*italics* or _italics_),
bold (**bold**),
typewritter text (`typewritter`)

Labels (1 point) all HTML documents should satisfy the following criteria:

assignments should be named assignment<x>_<y>.html where <x> is replaced by the assignment number and ` is replaced by your student number
Your full name, student number, assignment number, and course number should appear somewhere near the top of the rendered document
Questions should be labeled either by the use of headers or numbered lists.

Important

Submissions in any other format (e.g. Rmd, word document) will incur a 20% penalty.

Other Formats

Lab 05

Classification for Breast Cancer dataset

K-nearest neighbours classification

1. Compute Distances

2.A Simple Example Done Manually

Standardizing Data

Introduction to the tidymodels package in R

1. Preprocess the data

2. Build a model specification (model_spec) to specify the model and training algorithm

3. Put them together in a workflow and then fit it

4. Predict a new class label using predict

Assignment 4

General formating expectations

Introduction to the `tidymodels` package in R

2. Build a model specification (`model_spec`) to specify the model and training algorithm

3. Put them together in a workflow and then `fit` it

4. Predict a new class label using `predict`